
【题目】动圆![]() 与
与![]() 相外切,与
相外切,与![]() 相内切.
相内切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)![]() 是动圆
是动圆![]() 的半径最小时的圆,倾斜角为
的半径最小时的圆,倾斜角为![]() 且过点
且过点![]() 的直线l与
的直线l与![]() 相切,与轨迹
相切,与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】【选修4-4,坐标系与参数方程】
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为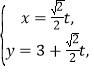 (t为参数),在以O为极点,
(t为参数),在以O为极点,![]() 轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]()
(Ⅰ)求直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(Ⅱ)若直线![]() 与
与![]() 轴的交点为P,直线
轴的交点为P,直线![]() 与曲线C的交点为A,B,求
与曲线C的交点为A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明).
的通项公式(不必证明).
(2)将数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值.
的值.
(3)设![]() 为数列
为数列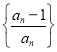 的前
的前![]() 项积,且
项积,且![]() ,求数列
,求数列![]() 的最大项.
的最大项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4,坐标系与参数方程】
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为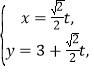 (t为参数),在以O为极点,
(t为参数),在以O为极点,![]() 轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]()
(Ⅰ)求直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(Ⅱ)若直线![]() 与
与![]() 轴的交点为P,直线
轴的交点为P,直线![]() 与曲线C的交点为A,B,求
与曲线C的交点为A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C的方程为![]() ,设AB是过椭圆C中心O的任意弦,l是线段AB的垂直平分线,M是l上与O不重合的点.
,设AB是过椭圆C中心O的任意弦,l是线段AB的垂直平分线,M是l上与O不重合的点.
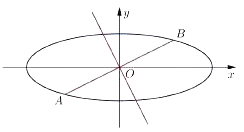
(1)求以椭圆的焦点为顶点,顶点为焦点的双曲线方程;
(2)若![]() ,当点A在椭圆C上运动时,求点M的轨迹方程;
,当点A在椭圆C上运动时,求点M的轨迹方程;
(3)记M是l与椭圆C的交点,若直线AB的方程为![]() ,当
,当![]() 面积取最小值时,求直线AB的方程;
面积取最小值时,求直线AB的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆过点
,且椭圆过点![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为实数,用
为实数,用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,
,![]() .对于函数
.对于函数![]() ,若存在
,若存在![]() 且
且![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 是“和谐”函数.
是“和谐”函数.
(1)判断函数![]() ,
,![]() 是否是“和谐”函数;(只需写出结论)
是否是“和谐”函数;(只需写出结论)
(2)设函数![]() 是定义在
是定义在![]() 上的周期函数,其最小周期为
上的周期函数,其最小周期为![]() ,若
,若![]() 不是“和谐”函数,求
不是“和谐”函数,求![]() 的最小值.
的最小值.
(3)若函数![]() 是“和谐”函数,求
是“和谐”函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某芯片公司对今年新开发的一批5G手机芯片进行测评,该公司随机调查了100颗芯片,并将所得统计数据分为![]() 五个小组(所调查的芯片得分均在
五个小组(所调查的芯片得分均在![]() 内),得到如图所示的频率分布直方图,其中
内),得到如图所示的频率分布直方图,其中![]() .
.
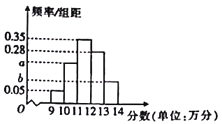
(1)求这100颗芯片评测分数的平均数(同一组中的每个数据可用该组区间的中点值代替).
(2)芯片公司另选100颗芯片交付给某手机公司进行测试,该手机公司将每颗芯片分别装在3个工程手机中进行初测。若3个工程手机的评分都达到11万分,则认定该芯片合格;若3个工程手机中只要有2个评分没达到11万分,则认定该芯片不合格;若3个工程手机中仅1个评分没有达到11万分,则将该芯片再分别置于另外2个工程手机中进行二测,二测时,2个工程手机的评分都达到11万分,则认定该芯片合格;2个工程手机中只要有1个评分没达到11万分,手机公司将认定该芯片不合格.已知每颗芯片在各次置于工程手机中的得分相互独立,并且芯片公司对芯片的评分方法及标准与手机公司对芯片的评分方法及标准都一致(以频率作为概率).每颗芯片置于一个工程手机中的测试费用均为300元,每颗芯片若被认定为合格或不合格,将不再进行后续测试,现手机公司测试部门预算的测试经费为10万元,试问预算经费是否足够测试完这100颗芯片?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com