
【题目】已知函数![]()
(1)当![]() 时,讨论函数
时,讨论函数![]() 零点的个数;
零点的个数;
(2)若![]() ,当
,当![]() =1时,求证:
=1时,求证:![]()
【答案】(1) 当 ![]() 时,函数
时,函数![]() 有两个不同的零点;当
有两个不同的零点;当![]() 时,函数
时,函数![]() 有且仅有一个零点;当
有且仅有一个零点;当![]() , 函数
, 函数![]() 没有零点.
没有零点.
(2)证明见解析.
【解析】试题分析:(1)对![]() 进行化简,构造函数
进行化简,构造函数![]() ,研究函数h(x)的单调性和最值,即可确定F(x)=f(x)﹣xlnx在定义域内是否存在零点;(2)由(Ⅰ)知,当a=1时f(x)在(0,+∞)上单调递增,要证明f(g(x))<f(x),只要证明g(x)<x即可.
,研究函数h(x)的单调性和最值,即可确定F(x)=f(x)﹣xlnx在定义域内是否存在零点;(2)由(Ⅰ)知,当a=1时f(x)在(0,+∞)上单调递增,要证明f(g(x))<f(x),只要证明g(x)<x即可.
详解:
(1)函数![]() 的定义域为
的定义域为![]()
由 ![]() 得
得![]()
令![]() 则
则![]()
由于![]() ,可知当
,可知当 ![]() 当
当![]() 时
时![]()
故函数![]() 在(0,1)上单调递减,在
在(0,1)上单调递减,在![]() 上单调递增,
上单调递增,
故![]() ,又
,又![]()
当 ![]() 时,函数
时,函数![]() 有两个不同的零点;
有两个不同的零点;
当![]() 时,函数
时,函数![]() 有且仅有一个零点;
有且仅有一个零点;
当![]() , 函数
, 函数![]() 没有零点.
没有零点.
(2)函数定义域为![]() 时,
时,![]()
由 ![]() 得:
得:![]()
![]() 时,
时,![]() 在
在![]() 上单调递增,且
上单调递增,且![]() 故对任意
故对任意![]()
所以,要证明![]() ,只需证:
,只需证:![]()
只需证:![]()
即证:![]()
即证;![]()
所以,要证明;![]()
令 ![]() 则
则![]()
故函数![]() 在
在![]() 上单调递增;
上单调递增;![]() ,
,![]()


科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.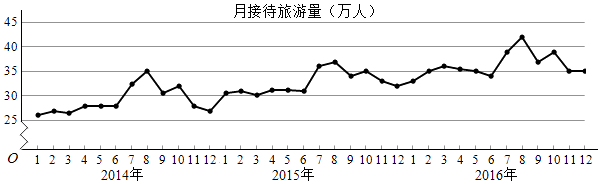
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)
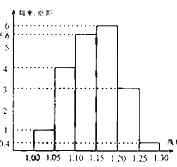
(Ⅰ)在答题卡上的表格中填写相应的频率;
(Ⅱ)估计数据落在(1.15,1.30)中的概率为多少;
(Ⅲ)将上面捕捞的100条鱼分别作一记号后再放回水库,几天后再从水库的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该水库中鱼的总条数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logax(a>1)在[a,2a]上的最大值是最小值的2倍.
(1)若函数g(x)=f(3x2-mx+5)在区间[-1,+∞)上是增函数,求实数m的取值范围;
(2)设函数F(x)=f(![]() )(2x),且关于x的方程F(x)=k在[
)(2x),且关于x的方程F(x)=k在[![]() ,4]上有解,求实数k的取值范围.
,4]上有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆N:x2+(y+ ![]() )2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,
)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0, ![]() )和DP上的点M,满足
)和DP上的点M,满足 ![]() =2
=2 ![]() ,
, ![]()
![]() =0.
=0. 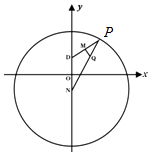
(1)当P在圆上运动时,求点Q的轨迹方程;
(2)若斜率为 ![]() 的直线l与(1)中所求Q的轨迹交于不同两点A、B,又点C(
的直线l与(1)中所求Q的轨迹交于不同两点A、B,又点C( ![]() ,2),求△ABC面积最大值时对应的直线l的方程.
,2),求△ABC面积最大值时对应的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某种商品在进价基础上每涨价1元,其销售量就减少10个,已知这种商品进价为40元/个,若按50元一个售出时能卖出500个.
(1)请写出售价x(![]() )元与利润y元之间的函数关系式;
)元与利润y元之间的函数关系式;
(2)试计算当售价定为多少元时,获得的利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1﹣x﹣ax2 . (Ⅰ)当a=0时,求证:f(x)≥0;
(Ⅱ)当x≥0时,若不等式f(x)≥0恒成立,求实数a的取值范围;
(Ⅲ)若x>0,证明(ex﹣1)ln(x+1)>x2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化.某调查机构随机抽取8名购物者进行采访,4名男性购物者中有3名倾向于网购,1名倾向于选择实体店,4名女性购物者中有2名倾向于选择网购,2名倾向于选择实体店.
(1)若从8名购物者中随机抽取2名,其中男女各一名,求至少1名倾向于选择实体店的概率:
(2)若从这8名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com