
【题目】已知函数 的图象恰好经过三个象限,则实数
的图象恰好经过三个象限,则实数![]() 的取值范围是______.
的取值范围是______.
【答案】![]() 或
或![]()
【解析】
分类讨论函数的单调性,计算![]() 在
在![]() 上的最小值,根据函数经过的象限得出最小值与零的关系,从而求出实数
上的最小值,根据函数经过的象限得出最小值与零的关系,从而求出实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,所以函数
,所以函数![]() 的图象经过第二、三象限,
的图象经过第二、三象限,
当![]() 时,
时,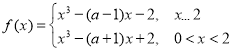 ,
,
所以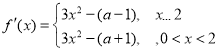 ,
,
①若![]() 时,
时,![]() 恒成立,又当
恒成立,又当![]() 时,
时,![]() ,所以函数
,所以函数![]() 图象在
图象在![]() 时,经过第一象限,符合题意;
时,经过第一象限,符合题意;
②若![]() 时,
时,![]() 在
在![]() 上恒成立,当
上恒成立,当![]() 时,令
时,令![]() ,解
,解![]() ,所以
,所以![]() 在
在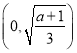 上单调递减,在
上单调递减,在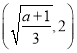 上单调递增,
上单调递增,
又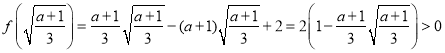
所以函数![]() 图象在
图象在![]() 时,经过第一象限,符合题意;
时,经过第一象限,符合题意;
(2)当![]() 时,
时,![]() 的图象在
的图象在![]() 上,只经过第三象限,
上,只经过第三象限,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 的图象在
的图象在![]() 上,只经过第一象限,故不符合题意;
上,只经过第一象限,故不符合题意;
(3)当![]() 时,
时,![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 的图象在
的图象在![]() 上只经过第三象限,所以
上只经过第三象限,所以![]() 在
在![]() 上的最小值
上的最小值![]() ,
,
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
若![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 上的最小值为
上的最小值为
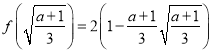 ,
,
令 .
.
若![]() 时,则
时,则![]() 在
在![]() 时,单调递减,
时,单调递减,
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
若![]() ,
,![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 在
在![]() 上的最小值为
上的最小值为![]() ,令
,令![]() ,所以
,所以![]() ;
;
若![]() ,
,![]() 在
在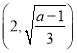 上单调递减,在
上单调递减,在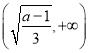 上单调递增,故
上单调递增,故![]() 在
在![]() 上的最小值为
上的最小值为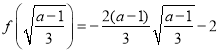 ,
,
显然![]() ,故
,故![]() ;
;
结上所述:![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
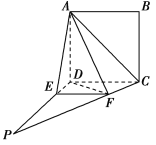
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
(1)证明:CF⊥平面ADF;
(2)求二面角DAFE的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市现有人口总数为100万人,如果年自然增长率为![]() 试回答下面的问题:
试回答下面的问题:
(1)写出该城市人口总数![]() (万人)与年份
(万人)与年份![]() (年)的函数关系式;
(年)的函数关系式;
(2)计算10年以后该城市人口总数(精确度为0.1万人);
(3)计算大约多少年以后该城市人口总数将达到120万人(精确度为1年).
(提示:![]() ;
;![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4这五个数字组成无重复数字的自然数.
(1)在组成的五位数中,所有奇数的个数有多少?
(2)在组成的五位数中,数字1和3相邻的个数有多少?
(3)在组成的五位数中,若从小到大排列,30124排第几个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() ,
,![]() ,C与l有且仅有一个公共点.
,C与l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)O为极点,A,B为C上的两点,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上恰有2个零点,求
上恰有2个零点,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,若
时,若![]() 对任意的正整数
对任意的正整数![]() 在区间
在区间![]() 上始终存在
上始终存在![]() 个整数使得
个整数使得![]() 成立,试问:正整数
成立,试问:正整数![]() 是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,点
为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,点![]() 在直线l:
在直线l:![]() 上.
上.
(1)求曲线C和直线l的直角坐标方程;
(2)若直线l与曲线C的相交于点A、B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com