
分析 此题考查的是函数与方程的综合应用类问题.在解答时,先结合存在性问题的特点先假设存在a符合题意,然后将问题转化为函数零点存在性的问题结合二次函数的特点即可获得问题的解答,注意验证.
解答 解:∵△=(3a-2)2-4(a-1)=9a2-16a+8>0,∴函数f(x)必有两个不相等的零点.
又函数f(x)的图象在区间(-1,3)上与x轴有且只有一个交点,
∴由零点存在性定理,可得f(-1)?f(3)≤0,即(2-2a)?(10a+2)≤0,解得a≤$-\frac{1}{5}$或a≥1.
因此存在实数$a∈(-∞,-\frac{1}{5}]∪[1,+∞)$满足题设条件.
点评 此题考查的是函数与方程的综合应用类问题.在解答的过程当中充分体现了函数与方程的思想、零点存在性知识以及结果验证的技巧.值得同学们体会反思.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{23}{25}$ | B. | $-\frac{2}{25}$ | C. | $-\frac{23}{25}$ | D. | $\frac{2}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
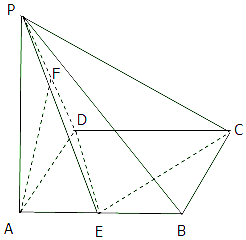 已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=3,F是PD的中点,E是线段AB上的点.
已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=3,F是PD的中点,E是线段AB上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com