
分析 (1)设椭圆方程为mx2+my2=1(m>0,n>0),代入A,B,C的坐标,解方程可得m,n,进而得到椭圆方程;
(2)运用三角形的面积公式和内切圆半径与三边周长的关系,结合当D在椭圆上顶点时,面积最大,求得半径的最大值,可得圆心坐标;
(3)将直线l:y=k(x-1)代入椭圆E的方程$\frac{x^2}{4}+\frac{y^2}{3}=1$,运用韦达定理,求得AM的方程和BN的方程与x=4的交点,证明它们重合即可得证.
解答 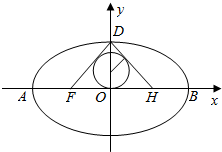 解:(1)设椭圆方程为mx2+my2=1(m>0,n>0),
解:(1)设椭圆方程为mx2+my2=1(m>0,n>0),
将A(-2,0)、B(2,0)、$C(1,\frac{3}{2})$代入椭圆E的方程,
得$\left\{\begin{array}{l}4m=1\\ m+\frac{9}{4}n=1\end{array}\right.$解得$m=\frac{1}{4},n=\frac{1}{3}$,
∴椭圆E的方程$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)|FH|=2,设△DFH边上的高为h,
${S_{△DFH}}=\frac{1}{2}×2×h=h$,
设△DFH的内切圆的半径为R,因为△DFH的周长为定值6.
所以$\frac{1}{2}R×6=3R={S_{△DFH}}$,
当D在椭圆上顶点时,h最大为$\sqrt{3}$,
故S△DFH的最大值为$\sqrt{3}$,
于是R也随之最大值为$\frac{{\sqrt{3}}}{3}$,
此时内切圆圆心的坐标为$(0,\frac{{\sqrt{3}}}{3})$;
(3)证明:将直线l:y=k(x-1)代入椭圆E的方程$\frac{x^2}{4}+\frac{y^2}{3}=1$,
并整理.得(3+4k2)x2-8k2x+4(k2-3)=0.
设直线l与椭圆E的交点M(x1,y1),N(x2,y2),
由根与系数的关系,得${x_1}+{x_2}=\frac{1}{{3+4{k^2}}},{x_1}{x_2}=\frac{{4({k^2}-3)}}{{3+4{k^2}}}$.
直线AM的方程为:$y=\frac{y_1}{{{x_1}+2}}(x+2)$,它与直线x=4的交点坐标为$p(4,\frac{{6{y_1}}}{{{x_1}+2}})$,
同理可求得直线BN与直线x=4的交点坐标为$Q(4,\frac{{2{y_2}}}{{{x_2}-2}})$.
下面证明P、Q两点重合,即证明P、Q两点的纵坐标相等.
∵y1=k(x1-1),y2=k(x2-1),
∴$\frac{{6{y_1}}}{{{x_1}+2}}-\frac{{2{y_2}}}{{{x_2}-2}}=\frac{{6k({x_1}-1)-({x_2}-2)-2k({x_2}-1)({x_1}+2)}}{{({x_1}+2)({x_2}-2)}}$
=$\frac{{2k[2{x_1}{x_2}-5({x_1}+{x_2})+8]}}{{({x_1}+2)({x_2}-2)}}=\frac{{2k[{\frac{{8({k^2}-3)}}{{3+4{k^2}}}-\frac{{40{k^2}}}{{3+4{k^2}}}+8}]}}{{({x_1}+2)({x_2}-2)}}=0$,
因此结论成立.
综上可知.直线AM与直线BN的交点住直线x=4上.
点评 本题考查椭圆的方程的求法,注意运用待定系数法,考查直线和椭圆方程联立,运用韦达定理,考查化简整理的运算能力,属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | ($\frac{6}{5}$,+∞) | D. | ($\frac{10}{9}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$-$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}-\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com