
已知函数f(x)=ex-ln(x+m).
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
(1)1(2)见解析
【解析】f′(x)=ex-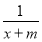 ,由x=0是f(x)的极值点,得f′(0)=0,所以m=1,
,由x=0是f(x)的极值点,得f′(0)=0,所以m=1,
于是f(x)=ex-ln(x+1),定义域为{x|x>-1},
f′(x)=ex-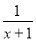 ,
,
函数f′(x)=ex-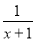 在(-1,+∞)上单递增,
在(-1,+∞)上单递增,
且f′(0)=0,
因此当x∈(-1,0)时,f′(x)<0;
当x∈(0,+∞)时,f′(x)>0.
所以f(x)在(-1,0)上单调递减,在(0,+∞)上单调递增.
(2)证明 当m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时,f(x)>0,
当m=2时,函数f′(x)=ex-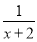 在(-2,+∞)上单调递增.
在(-2,+∞)上单调递增.
又f′(-1)<0,f′(0)>0,故f′(x)=0在(-2,+∞)上有唯一实根x0,且x0∈(-1,0).
当x∈(-2,x0)时,f′(x)<0;当x∈(x0,+∞)时,f′(x)>0,从而当x=x0时,f(x)取得最小值.
由f′(x0)=0,得ex0=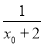 ,即ln(x0+2)=-x0,故f(x)≥f(x0)=
,即ln(x0+2)=-x0,故f(x)≥f(x0)=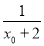 +x0=
+x0=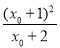 >0.综上,当m≤2时,f(x)>0.
>0.综上,当m≤2时,f(x)>0.


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:填空题
设y=f(x)是一次函数,f(0)=1,且f(1),f(4),f(13)成等比数列,则f(2)+f(4)+…+f(2n)=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:解答题
如图,过圆O外一点M作它的一条切线,切点为A,过A点作直线AP垂直直线OM,垂足为P.

(1)证明:OM·OP=OA2;
(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.证明:∠OKM=90°.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
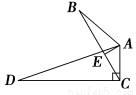
如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(解析版) 题型:选择题
已知函数f(x)=sin (2x+φ),其中φ为实数,若f(x)≤ 对x∈R恒成立,且
对x∈R恒成立,且 <f(π),则下列结论正确的是( ).
<f(π),则下列结论正确的是( ).
A. =-1
=-1
B.f >f
>f
C.f(x)是奇函数
D.f(x)的单调递增区间是 (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:填空题
关于x的方程x3-3x2-a=0有三个不同的实数解,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练4练习卷(解析版) 题型:解答题
已知函数f(x)=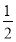 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R.
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:选择题
在平面直角坐标系xOy中,M为不等式组 所表示的区域上一动点,则直线OM斜率的最小值为( ).
所表示的区域上一动点,则直线OM斜率的最小值为( ).

A.2 B.1 C.-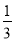 D.-
D.-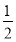
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:选择题
已知直线l交椭圆4x2+5y2=80于M,N两点,椭圆与y轴的正半轴交于B点,若△BMN的重心恰好落在椭圆的右焦点上,则直线l的方程是( ).
A.6x-5y-28=0 B.6x+5y-28=0
C.5x+6y-28=0 D.5x-6y-28=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com