
两个人射击,甲射击一次中靶概率是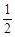 ,乙射击一次中靶概率是
,乙射击一次中靶概率是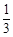 ,
,
(Ⅰ)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(Ⅱ)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
(Ⅲ)两人各射击5次,是否有99%的把握断定他们至少中靶一次?
(Ⅰ) (Ⅱ)
(Ⅱ) (Ⅲ)能断定
(Ⅲ)能断定
【解析】本题考查的知识点互斥事件的概率加法公式,对立事件的概率减法公式,n次独立重复试验中恰好发生k次的概率,在处理此类问题是,型清楚所求事件之间的关系,及所求事件是分类的(分几类?)还是分步的(分几步?)是解答的关键
(1)两人各射击一次,中靶至少一次就算完成目标,分成三种情况①乙中靶甲不中②甲中靶乙不中③甲乙全中,分别计算三种情况的概率,即可得到答案;
(2)两人各射击2次,中靶至少3次就算完成目标,分成两类情况,共击中3次和共击中4次,分别计算出每一类的概率,相加后,即可得到答案;
(3)我们可计算出两人各射击5次均不中的概率,进而根据对立事件概率减法公式,求出两人各射击5次,至少中靶一次的概率,比照后即可得到答案.
解 (Ⅰ)共三种情况:乙中靶甲不中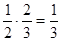 ;
甲中靶乙不中
;
甲中靶乙不中 ;
;
甲乙全 。 ∴概率是
。 ∴概率是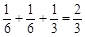 。
。
(Ⅱ)两类情况:
共击中3次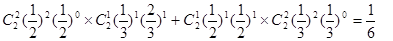 ;
;
共击中4次 ,
,
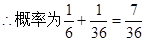 .
.
(III) ,能断定.
,能断定.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 5 |
| 4 |
| 1 |
| p1 |
| 1 |
| p2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)两个人射击,甲射击一次中靶概率是p1,乙射击一次中靶概率是p2,已知 , 是方程x2-5x + 6 = 0的根,若两人各射击5次,甲的方差是 .(1) 求 p1、p2的值;(2) 两人各射击2次,中靶至少3次就算完成目的,则完成目的的概率是多少?(3) 两人各射击一次,中靶至少一次就算完成目的,则完成目的的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com