
���� ���������������ԲC�ı�����Ϊ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$���ɵã�$c=1��\frac{c}{a}=\frac{{\sqrt{2}}}{2}$��b2=a2-c2��������ɵó���
��II����$\overrightarrow{EM}��\overrightarrow{EN}$���ɵ�$\overrightarrow{EM}•\overrightarrow{EN}=0$������m+1��2-n2=0���ɵ�M��m��n������Բ$\frac{x^2}{2}+{y^2}=1$�ϣ��ɵ�$\frac{m^2}{2}+{n^2}=1$����������ɵó���
��III������ֱ�ߵĽ��㡢һԪ���η��̵ĸ���ϵ���Ĺ�ϵ��������Բ��λ�ù�ϵ���ɵó���
��� �⣺���������������ԲC�ı�����Ϊ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$��
��$c=1��\frac{c}{a}=\frac{{\sqrt{2}}}{2}$����$c=1��a=\sqrt{2}$����2�֣�
��b2=a2-1=1����3�֣�
��ˣ��������ԲC�ı�����Ϊ$\frac{x^2}{2}+{y^2}=1$����4�֣�
������M��m��n����N��m��-n������$\overrightarrow{EM}=��m+1��n��$��$\overrightarrow{EN}=��m+1��-n��$��
��Ϊ$\overrightarrow{EM}��\overrightarrow{EN}$������$\overrightarrow{EM}•\overrightarrow{EN}=0$������m+1��2-n2=0�٣���5�֣���Ϊ��M��m��n������Բ$\frac{x^2}{2}+{y^2}=1$�ϣ�����$\frac{m^2}{2}+{n^2}=1$�ڣ� ��6�֣�
�ɢ٢ڽ�� $m=0��\;\;n=��1��m=-\frac{4}{3}��\;\;n=��\frac{1}{3}$�� ��7�֣�
��ˣ����������ĵ��У�0��1������0��-1����$��{-\frac{4}{3}��\frac{1}{3}}��$��$��{-\frac{4}{3}��-\frac{1}{3}}��$����8�֣�
����ֱ��MA�ķ���Ϊy��m-x1��=n��x-x1���ۣ�
ֱ��NB�ķ���Ϊy��m-x2��=-n��x-x2���ܣ���9�֣�
��ֱ��MA��ֱ��NB����ΪP��x0��y0���������������ۡ��ܲ��������ã�y0-n��x1=my0-nx0��
��y0+n��x2=my0+nx0�ޣ�10�֣�
�������˵� $��y_0^2-{n^2}��{x_1}{x_2}={m^2}y_0^2-{n^2}x_0^2$�ߣ���11�֣�
��x1x2=2��m2=2-2n2���������� $x_0^2+2y_0^2=2$��
��ˣ�ֱ��MA��ֱ��NB�Ľ���P������ԲC�ϣ���12�֣�
���� ���⿼������Բ�ı����̼������ʡ�������ֱ���������Ĺ�ϵ��һԪ���η��̵ĸ���ϵ���Ĺ�ϵ����������������������������������⣮


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 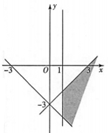 | B�� | 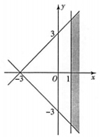 | C�� | 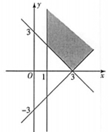 | D�� | 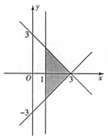 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com