Question

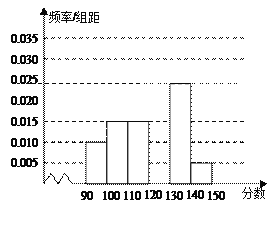
【题目】某校从参加高二某次月考的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六组后得到如右所示的部分频率分布直方图。观察图形信息，回答下列问题：

（Ⅰ）求分数在内的频率；

（Ⅱ）用分层抽样的方法在分数段的学生中抽取一个容量为6的样本，再从该样本中任取2人，求至多有1人在分数段内的概率。

Answer 1

【答案】（1）0.3（2）

【解析】试题分析：（Ⅰ）根据频率分别直方图的面积表示频率，并且所以小矩形的面积之和等于，来求的面积，就是频率；（Ⅱ）第一步，先跟两个分数段的频率，就是两个分数段的学生人数，第二步，计算分层比，计算两个分数段的各应抽取的人数，第三步，将这所抽取到的人分别编号，然后列举所有抽取到的组合情况，至多有1人在分数段[120,130）内组合数，按古典概型计算概率．

试题解析：（Ⅰ）[120,130）内的频率为；…5分

（Ⅱ）由题意，[110,120）分数段的人数为60×0．15＝9（人）．[120,130）分数段的人数为60×0．3＝18（人）．

∵用分层抽样的方法在分数段为[110,130）的学生中抽取一个容量为6的样本，

∴需在[110,120）分数段内抽取2人，并分别记为、；

在[120,130）分数段内抽取4人，并分别记为、、、；

设“从样本中任取2人，至多有1人在分数段[120,130）内”为事件A，则基本事件共有， 共15种．

则事件A包含的基本事件有， 共9种．

∴．