
【题目】设函数f(x)=2cos2x+ ![]() sin2x﹣1.
sin2x﹣1.
(1)求f(x)的最大值及此时的x值
(2)求f(x)的单调减区间
(3)若x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
【答案】
(1)解:f(x)=2cos2x+ ![]() sin2x﹣1=cos2x+
sin2x﹣1=cos2x+ ![]() =
= ![]() ,
,
当2x+ ![]() ,即
,即 ![]() 时,f(x)max=2
时,f(x)max=2
(2)解:由 ![]() ,得
,得 ![]() ,
,
∴f(x)的单调减区间为[ ![]() ],k∈Z
],k∈Z
(3)解: ![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
∴ ![]() ,
,
∴﹣1≤f(x)≤2.
则f(x)的值域为[﹣1,2]
【解析】f(x)=2cos2x+ ![]() sin2x﹣1=cos2x+
sin2x﹣1=cos2x+ ![]() =
= ![]() (1)当2x+
(1)当2x+ ![]() ,即
,即 ![]() 时,f(x)取得最大值;(2)由
时,f(x)取得最大值;(2)由 ![]() ,得
,得 ![]() ,即可求出f(x)的单调减区间;(3)由
,即可求出f(x)的单调减区间;(3)由 ![]() ,得
,得 ![]() ,即可求出f(x)的值域.
,即可求出f(x)的值域.
【考点精析】本题主要考查了正弦函数的单调性和三角函数的最值的相关知识点,需要掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;函数
上是减函数;函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】根据下列条件,分别求直线方程:
(1)经过点A(3,0)且与直线2x+y﹣5=0垂直;
(2)求经过直线x﹣y﹣1=0与2x+y﹣2=0的交点,且平行于直线x+2y﹣3=0的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+lnx(a∈R).
(1)当a=![]() 时,求f(x)在区间[1,e]上的最大值和最小值;
时,求f(x)在区间[1,e]上的最大值和最小值;
(2)如果函数g(x),f1(x),f2(x),在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x),f2(x)的“活动函数”.已知函数![]() .
. ![]() 。若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围.
。若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,c= ![]() asinC﹣ccosA.
asinC﹣ccosA.
(1)求A;
(2)若a=2,△ABC的面积为 ![]() ,求b,c.
,求b,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|2﹣5≤2﹣x≤4},B={x|x2+2mx﹣3m2<0,m>0}.
(1)若m=2,求A∩B;
(2)若BA,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图. 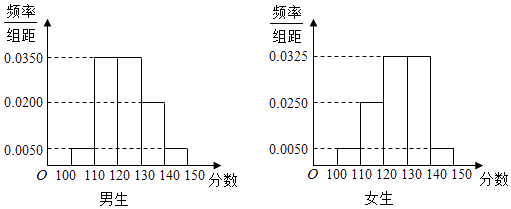
附:K2= ![]() .
.
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 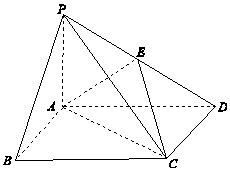
(1)证明:PB∥平面AEC;
(2)设AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,求二面角D﹣AE﹣C的大小.
,求二面角D﹣AE﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位: ![]() )和年利润
)和年利润![]() (单位:千元)的影响.对近8年的年宣传费
(单位:千元)的影响.对近8年的年宣传费![]() 和年销售量
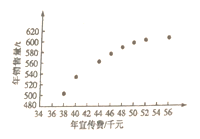
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
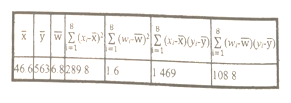
表中![]() .
.
(1)根据散点图判断![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归类型?(给出判断即可,不必说明理由)
的回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的利润![]() 与
与![]() 的的关系为
的的关系为![]() .根据(2)的结果回答下列问题:
.根据(2)的结果回答下列问题:
(ⅰ)年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的的斜率和截距的最小二乘估计为
的的斜率和截距的最小二乘估计为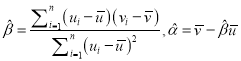 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com