
【题目】抽样调查某大型机器设备使用年限x和该年支出维修费用y(万元),得到数据如表
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
部分数据分析如下 ![]() =25,
=25, ![]() yi=112.3,
yi=112.3, ![]() =90
=90
参考公式:线性回归直线方程为 ![]() ,
, 
(1)求线性回归方程;
(2)由(1)中结论预测第10年所支出的维修费用.
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知四棱柱![]() 的底面是边长为
的底面是边长为![]() 的菱形,且
的菱形,且![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,设
,设![]() 为
为![]() 的中点。
的中点。
(Ⅰ)求证: ![]() 平面
平面![]()
(Ⅱ)点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,
,
求平面 和平面
和平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C1的参数方程为 ![]() (φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4
(φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4 ![]() cosθ.
cosθ.
(1)求C1与C2交点的直角坐标;
(2)已知曲线C3的参数方程为 ![]() (0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
(0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一曲线C是与两个定点O(0,0),A(3,0)的距离比为 ![]() 的点的轨迹.
的点的轨迹.
(1)求曲线C的方程,并指出曲线类型;
(2)过(﹣2,2)的直线l与曲线C相交于M,N,且|MN|=2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. 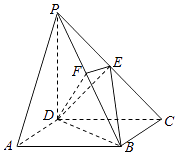
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com