
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某中学举行的“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如下表,该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中一等奖代表队有6人.
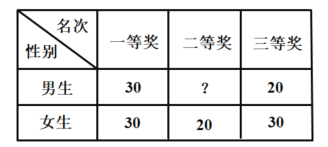
(1)求二等奖代表队的男生人数;
(2)从前排就坐的三等奖代表队员5人(2男3女)中随机抽取3人上台领奖,请求出只有一个男生上台领奖的概率;
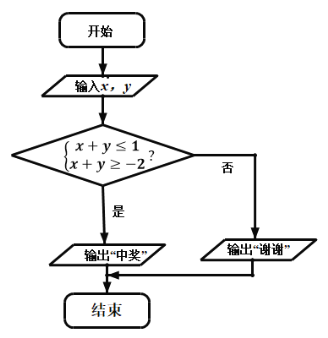
(3)抽奖活动中,代表队员通过操作按键,使电脑自动产生[![]() 2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PAPD,E,F分别为AD,PB的中点.求证:
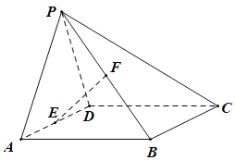
(1)EF//平面PCD;
(2)平面PAB平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学计划用他姓名的首字母![]() ,身份证的后4位数字(4位数字都不同)以及3个符号
,身份证的后4位数字(4位数字都不同)以及3个符号![]() 设置一个六位的密码.若
设置一个六位的密码.若![]() 必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
A.864B.1009C.1225D.1441
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上的点到准线的最小距离为
上的点到准线的最小距离为![]() .
.
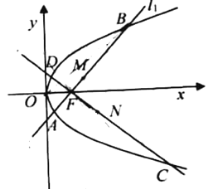
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 、
、![]() ,
,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 分别为弦
分别为弦![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程:
的参数方程: (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过曲线![]() 上一点
上一点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,中点为
两点,中点为![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司A产品生产的投入成本x(单位:万元)与产品销售收入y(单位:十万元)存在较好的线性关系,下表记录了该公司最近8次该产品的相关数据,且根据这8组数据计算得到y关于x的线性回归方程为![]() .
.
x(万元) | 6 | 7 | 8 | 11 | 12 | 14 | 17 | 21 |
y(十万元) | 1.2 | 1.5 | 1.7 | 2 | 2.2 | 2.4 | 2.6 | 2.9 |
(1)求![]() 的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
(2)该公司B产品生产的投入成本u(单位:万元)与产品销售收入v(单位:十万元)也存在较好的线性关系,且v关于u的线性回归方程为![]() .
.
(i)估计该公司B产品投入成本30万元后的毛利率(毛利率![]() );
);
(ii)判断该公司A,B两个产品都投入成本30万元后,哪个产品的毛利率更大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的归家之一,某市为了制订合理的节水方案,对家庭用水情况进行了抽样调查,获得了某年100个家庭的月均用水量(单位:![]() )的数据,将这些数据按照
)的数据,将这些数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
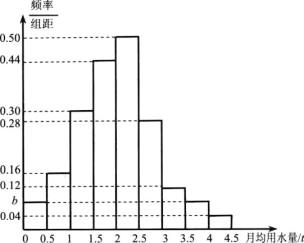
(1)求图中的![]() 值,若该市有30万个家庭,试估计全市月均用水量不低于
值,若该市有30万个家庭,试估计全市月均用水量不低于![]() 的家庭数;
的家庭数;
(2)假设同组中的每个数据都用该组区间的中点值代替,试估计全市家庭月均用水量的平均数;
(3)现从月均用水量在![]() ,
,![]() 的家庭中,先按照分层抽样的方法抽取9个家庭,再从这9家庭中抽取4个家庭,记这4个家庭中月均用水量在
的家庭中,先按照分层抽样的方法抽取9个家庭,再从这9家庭中抽取4个家庭,记这4个家庭中月均用水量在![]() 中的数量为
中的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com