
 ,
,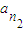 ,…,
,…,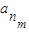 是公差为d的等差数列{an}中的任意m个项,若
是公差为d的等差数列{an}中的任意m个项,若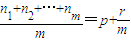 (0≤r<m,p、r、m∈N或r=0)①,则有
(0≤r<m,p、r、m∈N或r=0)①,则有 ②,特别地,当r=0时,称ap为
②,特别地,当r=0时,称ap为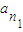 ,
,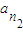 ,…,
,…,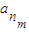 的等差平均项.
的等差平均项.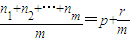 ,可化为
,可化为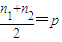 ,
,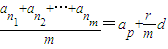 可化为
可化为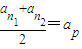 ;
;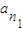 ,
,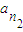 ,…,
,…,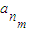 是公比为q的等比数列{an}中的任意m个项,若
是公比为q的等比数列{an}中的任意m个项,若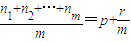 (0≤r<m,p、r、m∈N或r=0①,则有
(0≤r<m,p、r、m∈N或r=0①,则有 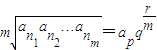 ②,特别地,当r=0时,称ap为
②,特别地,当r=0时,称ap为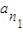 ,
,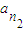 ,…,
,…,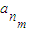 的等比平均项.
的等比平均项.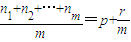 (0≤r<m,p、r、m∈N或r=0)①,
(0≤r<m,p、r、m∈N或r=0)①,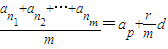 ②,
②,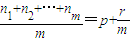 ,可化为
,可化为 ,
,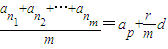 可化为
可化为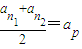 ;
;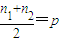 ,则
,则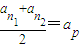 .
.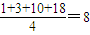 ,
,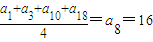 .
.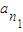 ,
,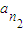 ,…,
,…, 是公差为d的等差数列{an}中的任意m个项,
是公差为d的等差数列{an}中的任意m个项,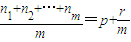 (0≤r<m,p、r、m∈N或r=0)①,
(0≤r<m,p、r、m∈N或r=0)①,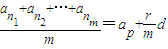 ②,
②,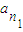 ,
,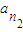 ,…,
,…,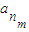 的等差平均项.
的等差平均项.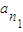 ,
,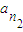 ,…,
,…,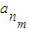 是公比为q的等比数列{an}中的任意m个项,
是公比为q的等比数列{an}中的任意m个项,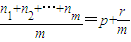 (0≤r<m,p、r、m∈N或r=0①,
(0≤r<m,p、r、m∈N或r=0①, ②,
②,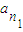 ,
,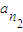 ,…,
,…,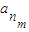 的等比平均项.
的等比平均项.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
| OP |
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 4a |
| x2 |
| 16 |
| y2 |
| 9 |
| x2 |
| 35-λ |
| y2 |
| 10-λ |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| n1+n2+…+nm |
| m |
| r |
| m |
| an1+an2+…+anm |
| m |
| r |
| m |
查看答案和解析>>
科目:高中数学 来源:2007年南通市教研室高三数学考前预测题 题型:044
有以下真命题:设![]() ,
,![]() ,…,
,…,![]() 是公差为d的等差数列{an}中的任意m个项,若
是公差为d的等差数列{an}中的任意m个项,若![]() (0≤r<m,p、r、m∈N或r=0)①,则有
(0≤r<m,p、r、m∈N或r=0)①,则有![]() ②,特别地,当r=0时,称
②,特别地,当r=0时,称![]() 为
为![]() ,
,![]() ,…,
,…,![]() 的等差平均项.
的等差平均项.
(1)当m=2,r=0时,试写出与上述命题中的(1),(2)两式相对应的等式;
(2)已知等差数列{an}的通项公式为an=2n,试根据上述命题求a1,a3,a10,a18的等差平均项;
(3)试将上述真命题推广到各项为正实数的等比数列中,写出相应的真命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com