
分析 (I)利用等差数列的前n项和,求出公差,然后求数列{an},利用求和公式,转化求解{bn}的通项公式;
(II)化简cn=lnbn+(-1)nlnSn,然后求解数列{cn}的前n项和Mn.
解答 解:(Ⅰ)∵{an}是等差数列,∴${S_5}=5{a_1}+\frac{5×4}{2}d⇒30=5×2+10d⇒d=2$,
∴an=2n…(3分)
数列{bn}的前n项和为Tn,且${T_n}={2^n}-1$,
∴b1=1,n≥2时${b_n}={T_n}-{T_{n-1}}={2^{n-1}}$,
∴${b_n}={2^{n-1}}(n∈{N^*})$…(6分)
(Ⅱ)${S_n}=2•\frac{n(n+1)}{2}=n(n+1)$…(7分)
${c_n}=ln{b_n}+{(-1)^n}ln{S_n}=ln({2^{n-1}})+{(-1)^n}ln[n(n+1)]$=(n-1)ln2+(-1)n[lnn+ln(n+1)]…(8分)
∴${M_n}=ln2×[0+1+2+…+(n-1)]+{N_n}=\frac{n(n-1)}{2}ln2+{N_n}$
其中${N_n}=-(ln1+ln2)+(ln2+ln3)-(ln3+ln4)+…+{(-1)^n}[lnn+ln(n+1)]$=(-1)nln(n+1)…(10分)∴${M_n}=\frac{n(n-1)}{2}ln2+{(-1)^n}ln(n+1)$…(12分)
点评 本题考查数列求和等差数列和的应用,数列的递推关系式的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
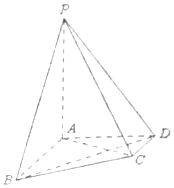 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,PA⊥平面ABCD,PA=4.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,PA⊥平面ABCD,PA=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com