
【题目】为了了解学生考试时的紧张程度,现对100名同学进行评估,打分区间为![]() ,得到频率分布直方图如下,其中
,得到频率分布直方图如下,其中![]() 成等差数列,且
成等差数列,且![]() .
.
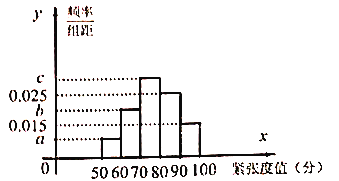
(1)求![]() 的值;
的值;
(2)现采用分层抽样的方式从紧张度值在![]() ,
,![]() 中共抽取5名同学,再从这5名同学中随机抽取2人,求至少有一名同学是紧张度值在
中共抽取5名同学,再从这5名同学中随机抽取2人,求至少有一名同学是紧张度值在![]() 的概率.
的概率.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的极坐标方程和
的极坐标方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与曲线
与曲线![]() 分别交于第一象限内的
分别交于第一象限内的![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使不等式f(x)≥2x-3对任意x∈R恒成立?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面![]() 个说法中正确的序号为_____.
个说法中正确的序号为_____.
①函数![]() 有两个零点;
有两个零点;
②函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
③若![]() 是第三象限角,则
是第三象限角,则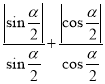 的取值集合为
的取值集合为![]() ;
;
④锐角三角形![]() 中一定有
中一定有![]() ;
;
⑤已知![]() (
(![]() 且
且![]() ),同一平面内有
),同一平面内有![]() 、
、![]() 、
、![]() 、
、![]() 四个不同的点,若
四个不同的点,若![]() ,则
,则![]() 、
、![]() 、
、![]() 必定三点共线.
必定三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知函数![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴的交点,
轴的交点,![]() 、
、![]() 分别是
分别是![]() 的图象上横坐标为
的图象上横坐标为![]() 、
、![]() 的两点,
的两点,![]() 轴,且
轴,且![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
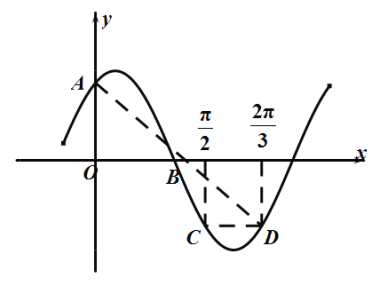
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)若关于![]() 的函数
的函数![]() 在区间
在区间![]() 上恰好有一个零点,求实数
上恰好有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 是函数
是函数![]() 的反函数.
的反函数.
![]() 求函数
求函数![]() 的解析式,并写出定义域
的解析式,并写出定义域![]() ;
;
![]() 设
设![]() ,判断并证明函数
,判断并证明函数![]() 在区间
在区间![]() 上的单调性:
上的单调性:
![]() 若
若![]() 中的函数
中的函数![]() 在区间
在区间![]() 内的图像是不间断的光滑曲线,求证:函数
内的图像是不间断的光滑曲线,求证:函数![]() 在区间
在区间![]() 内必有唯一的零点(假设为
内必有唯一的零点(假设为![]() ),且
),且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的参数方程;
的参数方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com