
分析 根据已知中函数的解析式,结合函数奇偶性的定义,先判断函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,进而可得答案.
解答 解:(1)函数f(x)=(x-1)$\sqrt{\frac{x+1}{x-1}}$的定义域为(-∞,-1]∪(1,+∞)不关于原点对称,
故函数f(x)=(x-1)$\sqrt{\frac{x+1}{x-1}}$为非奇非偶函数;
(2)函数f(x)=$\sqrt{1+{x}^{2}}-x$的定义域R关于原点对称,
f(-x)=$\sqrt{1+{(-x)}^{2}}+x$=$\sqrt{1+{x}^{2}}+x$.
f(-x)=f(x)和f(-x)=-f(x)均不成立,
故函数f(x)=$\sqrt{1+{x}^{2}}-x$为非奇非偶函数.
点评 本题考查的知识点是函数奇偶性的判断,正确理解函数奇偶性的定义,是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,2] | C. | (1,$\sqrt{3}$] | D. | (1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
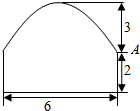 一条隧道横截面由一段抛物线及矩形的三边围成,各段长度见图中所示(单位:米),某卡车空载时可通过此隧道.
一条隧道横截面由一段抛物线及矩形的三边围成,各段长度见图中所示(单位:米),某卡车空载时可通过此隧道.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M、N分别是A B.PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M、N分别是A B.PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com