
【题目】如图所示,正四棱锥![]() 中,
中,![]() 为底面正方形的中心,侧棱
为底面正方形的中心,侧棱![]() 与底面
与底面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.

(1)求侧面![]() 与底面
与底面![]() 所成的二面角的大小;
所成的二面角的大小;
(2)若![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(3)问在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ⊥侧面
⊥侧面![]() ,若存在,试确定点
,若存在,试确定点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥平面A1BD;
(2)求锐二面角A-A1D-B的余弦值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下间题:“今有甲、乙、丙、丁、戊五人分五饯,令上二人所得与下三人等,且五人所得钱按顺序等次差,问各得几何?”其意思为“甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱(钱:古代一种重量单位)?”这个问题中丙所得为( )
A. ![]() 钱 B.
钱 B. ![]() 钱 C. 1钱 D.
钱 C. 1钱 D. ![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有3个白球,4个黑球,从中任取3个球,则
①恰有1个白球和全是白球;
②至少有1个白球和全是黑球;
③至少有1个白球和至少有2个白球;
④至少有1个白球和至少有1个黑球.
在上述事件中,是互斥事件但不是对立事件的为( )
A.②B.①C.③D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取![]() 名进行调查,将受访用户按年龄分成
名进行调查,将受访用户按年龄分成![]() 组:
组: ![]() ,
, ![]() ,…,
,…, ![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于![]() 岁的概率;
岁的概率;
(Ⅲ)估计春节期间参与收发网络红包的手机用户的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解本校学生网课期间课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.
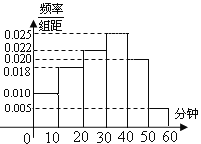
(1)根据频率分布直方图估计抽取样本的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)已知样本中玩电脑游戏时长在![]() 的学生中,男生比女生多1人,现从中任选3人进行回访,求选出的3人中恰有两人是男生的概率.
的学生中,男生比女生多1人,现从中任选3人进行回访,求选出的3人中恰有两人是男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com