练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数f(x)=6-
    		x2+9
    的值域是（　　）
    A、（-∞，6]
    B、（-∞，3]
    C、（0，6]
    D、（0，3]
    分析：此题宜用换元法求值域，先令t=x2，将函数f(x)=6-
    		x2+9
    变为y=6-
    		t+9
    ，t∈[0，+∞），利用单调性求值域即可．
    解答：解：令t=x2，则函数f(x)=6-
    		x2+9
    变为y=6-
    		t+9
    ，t∈[0，+∞），
    由函数的解析式知：y=6-
    		t+9
    ，在[0，+∞）是减函数，其最大值是6-
    		0+9
    =3，
    故函数y=6-
    		t+9
    ，在[0，+∞）上的值域是（-∞，3]，
    即函数f(x)=6-
    		x2+9
    的值域（-∞，3]，
    故应选B．
    点评：本题考点是函数的值域，由此函数是一偶函数，故在解决此题时先用换元法将其变成了单调函数，大大降低了求值域的难度，做题时要注意这样的技巧的运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数f(x)=
    		3
    sinxcosx+cos2x+a    ．
    （Ⅰ）写出函数的最小正周期及单调递减区间；
    （Ⅱ）当x∈[-
    π
    6
    ，
    π
    3
    ]时，函数f（x）的最大值与最小值的和为
    3
    2
    ，求f（x）的解析式；
    （Ⅲ）将满足（Ⅱ）的函数f（x）的图象向右平移
    π
    12
    个单位，纵坐标不变横坐标变为原来的2倍，再向下平移
    1
    2
    ，得到函数g（x），求g（x）图象与x轴的正半轴、直线x=
    π
    2
    所围成图形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    对于函数f(x)，x∈[a，b]及g(x)，x∈[a，b]。若对任意的x∈[a，b]，总有，我们称f(x)可被g(x)替代，那么下列给出的函数中能替代的是(    )

    A．g(x)=x+6，x∈[4，16]

    B．g(x)=x2+6，x∈[4，16]

    C．g(x)=(x+6)，x∈[4，16]

    D．g(x)=2x+6，x∈[4，16]

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    对于函数f(x)，x∈[a，b]及g(x)，x∈[a，b]。若对任意的x∈[a，b]，总有，我们称f(x)可被g(x)替代，那么下列给出的函数中能替代的是(    )

    A．g(x)=x+6，x∈[4，16]

    B．g(x)=x2+6，x∈[4，16]

    C．g(x)=(x+6)，x∈[4，16]

    D．g(x)=2x+6，x∈[4，16]

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练17练习卷（解析版） 题型：选择题

    已知函数f(x)=2sin(ωx+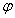),x∈R,其中ω>0,-π<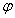≤π.若f(x)的最小正周期为6π,且当x=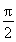时,f(x)取得最大值,则(　　)

    (A)f(x)在区间[-2π,0]上是增函数

    (B)f(x)在区间[-3π,-π]上是增函数

    (C)f(x)在区间[3π,5π]上是减函数

    (D)f(x)在区间[4π,6π]上是减函数

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设函数f(x)=
    		3
    sinxcosx+cos2x+a    ．
    （Ⅰ）写出函数的最小正周期及单调递减区间；
    （Ⅱ）当x∈[-
    π
    6
    ，
    π
    3
    ]时，函数f（x）的最大值与最小值的和为
    3
    2
    ，求f（x）的解析式；
    （Ⅲ）将满足（Ⅱ）的函数f（x）的图象向右平移
    π
    12
    个单位，纵坐标不变横坐标变为原来的2倍，再向下平移
    1
    2
    ，得到函数g（x），求g（x）图象与x轴的正半轴、直线x=
    π
    2
    所围成图形的面积．

    查看答案和解析>>

    同步练习册答案