
【题目】设数列{an}的前n项和为Sn . 若对n∈N* , 总k∈N* , 使得Sn=ak , 则称数列{an}是“G数列”. (Ⅰ)若数列{an}是等差数列,其首项a1=1,公差d=﹣1.证明:数列{an}是“G数列”;
(Ⅱ)若数列{an}的前n项和Sn=3n(n∈N*),判断数列{an}是否为“G数列”,并说明理由;
(Ⅲ)证明:对任意的等差数列{an},总存在两个“G数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
【答案】解:(1)证明:由题意an=1+(n﹣1)(﹣1)=2﹣n, ![]() ,
,
若 ![]() ,
,
则 ![]() .
.
所以,存在k∈N* , 使得Sn=ak .
所以,数列{an}是“G数列.
(Ⅱ)首先a1=S1=3,
当n≥2时, ![]() ,
,
所以 ![]()
当n=2时,9=2×3k﹣1 , 得kN*因此数列{an}不是“G数列”.
(Ⅲ)若dn=bn,(b为常数),
则数列{dn}的前n项和 ![]() 是数列{dn}中的第
是数列{dn}中的第 ![]() 项,因此数列{dn}是“G数列”.
项,因此数列{dn}是“G数列”.
对任意的等差数列{an},an=a1+(n﹣1)d,(d为公差),
设bn=na1 , cn=(d﹣a1)(n﹣1),
则an=bn+cn , 而数列{bn}和{cn}都是“G数列”.
【解析】(Ⅰ)根据G数列的定义证明即可,(Ⅱ)由 ![]() ,可以判断数列{an}不是“G数列”,(Ⅲ)若dn=bn,(b为常数),可与判断数列{dn}是“G数列”,继而可以证明an=bn+cn(n∈N*)成立.
,可以判断数列{an}不是“G数列”,(Ⅲ)若dn=bn,(b为常数),可与判断数列{dn}是“G数列”,继而可以证明an=bn+cn(n∈N*)成立.
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系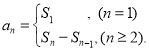 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 从
从![]() ,
, ![]() ,
, ![]() ,
, ![]() 四个数中任取的一个数,
四个数中任取的一个数, ![]() 是从
是从![]() ,
, ![]() ,
, ![]() 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司购买了一块长AM=30米,宽AN=20米的矩形地块,计划把图中矩形ABCD建设为仓库,其余地方为道路和停车场,要求顶点C在地块对角线MN上,B、D分别在边AM、AN上,假设AB的长度为x米
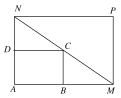
(1)求矩形ABCD的面积S关于x的函数解析式;
(2)要使仓库占地ABCD的面积不少于144平方米,则AB的长度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,函数g(x)=f(x)﹣k.
,函数g(x)=f(x)﹣k.
(1)当m=2时,若函数g(x)有两个零点,则k的取值范围是;
(2)若存在实数k使得函数g(x)有两个零点,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.
(I)求证:EM⊥AD;
(II)求二面角A﹣BE﹣C的余弦值;
(III)在线段EC上是否存在点P,使得直线AP与平面ABE所成的角为45°,若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,{bn}是等比数列,其中a1=b1=1,a2≠b2,且b2为a1、a2的等差中项,a2为b2、b3的等差中项.
(1)求数列{an}与{bn}的通项公式;
(2)记![]() ,求数列{cn}的前n项和Sn.
,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an=logn(n+1)(n≥2,n∈N*).定义:使乘积a1·a2·a3……ak为正整数的k(k∈N*)叫做“和谐数”,则在区间[1,2018]内所有的“和谐数”的和为
A. 2036 B. 2048 C. 4083 D. 4096
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|.
(Ⅰ)若不等式f(x)≤2的解集为[0,4],求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若x0∈R,使得f(x0)+f(x0+5)﹣m2<4m,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin![]()
(A>0,ω>0)的最小值为-2,其图象相邻两个对称中心之间的距离为![]() .
.
(1)求f(x)的最小正周期及对称轴方程;
(2)若f![]() ,求f
,求f![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com