
 =
=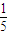 .从而P(ξ=k)=C10k(
.从而P(ξ=k)=C10k(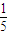 )k(
)k( )10-k,k=0,1,2,…,10.
)10-k,k=0,1,2,…,10. )10+C101•
)10+C101• •(
•( )9+C102(
)9+C102( )2•(
)2•( )8
)8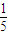 )3(
)3( )7+C104(
)7+C104(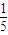 )4•(
)4•(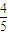 )6+C105(
)6+C105( )5•(
)5•( )5≈0.994.
)5≈0.994.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)现因当地电力供应紧张,供电部门只提供50千瓦的电力,这10台机床能够正常工作的概率为多大?
(2)在一个工作班的8个小时内,不能正常工作的时间大约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com