
【题目】函数y=f(x)图像上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)= ![]() 叫曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: (1.)函数y=x3﹣x2+1图像上两点A、B的横坐标分别为1,2,则φ(A,B)>
叫曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: (1.)函数y=x3﹣x2+1图像上两点A、B的横坐标分别为1,2,则φ(A,B)> ![]() ;
;
(2.)存在这样的函数,图像上任意两点之间的“弯曲度”为常数;
(3.)设点A、B是抛物线,y=x2+1上不同的两点,则φ(A,B)≤2;
(4.)设曲线y=ex上不同两点A(x1 , y1),B(x2 , y2),且x1﹣x2=1,若tφ(A,B)<1恒成立,则实数t的取值范围是(﹣∞,1);
以上正确命题的序号为(写出所有正确的)
【答案】(2)(3)
【解析】解:对于(1),由y=x3﹣x2+1,得y′=3x2﹣2x,则 ![]() ,
, ![]() ,
,
y1=1,y2=5,则 ![]() ,
,
φ(A,B)= ![]() ,(1)错误;
,(1)错误;
对于(2),常数函数y=1满足图像上任意两点之间的“弯曲度”为常数,(2)正确;
对于(3),设A(x1 , y1),B(x2 , y2),y′=2x,
则kA﹣kB=2x1﹣2x2 , ![]() =
= ![]()
= ![]() .
.
∴φ(A,B)=  =
= 
![]() ,(3)正确;
,(3)正确;
对于(4),由y=ex , 得y′=ex , φ(A,B)=  =
=  .
.
tφ(A,B)<1恒成立,即 ![]() 恒成立,t=1时该式成立,∴(4)错误.
恒成立,t=1时该式成立,∴(4)错误.
所以答案是:(2)(3).
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案,需要熟知两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


科目:高中数学 来源: 题型:
【题目】若a、b、c是常数,则“a>0且b2﹣4ac<0”是“对任意x∈R,有ax2+bx+c>0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知角A、B、C所对的边分别为a、b、c,且a2+b2﹣c2= ![]() ab.
ab. 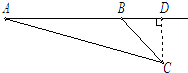
(1)求角C的大小;
(2)如果0<A≤ ![]() ,m=2cos2
,m=2cos2 ![]() ﹣sinB﹣1,求实数m的取值范围.
﹣sinB﹣1,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x3+x(x∈R),当 ![]() 时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
A.(﹣∞,1)
B.(﹣∞,0)
C.(﹣∞, ![]() )
)
D.(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+ ![]() ﹣2)(a>0) (Ⅰ)当1<a<4时,函数f(x)在[2,4]上的最小值为ln
﹣2)(a>0) (Ⅰ)当1<a<4时,函数f(x)在[2,4]上的最小值为ln ![]() ,求a;
,求a;
(Ⅱ)若存在x0∈(2,+∞),使得f(x0)<0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先把正弦函数y=sinx图象上所有的点向左平移 ![]() 个长度单位,再把所得函数图象上所有的点的纵坐标缩短到原来的
个长度单位,再把所得函数图象上所有的点的纵坐标缩短到原来的 ![]() 倍(横坐标不变),再将所得函数图象上所有的点的横坐标缩短到原来的
倍(横坐标不变),再将所得函数图象上所有的点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),则所得函数图象的解析式是( )
倍(纵坐标不变),则所得函数图象的解析式是( )
A.y=2sin( ![]() x+
x+ ![]() )
)
B.y= ![]() sin(2x﹣
sin(2x﹣ ![]() )
)
C.y=2sin( ![]() x﹣
x﹣ ![]() )
)
D.y= ![]() sin(2x+
sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,sinx),
=(sinx,sinx), ![]() =(﹣1,0)
=(﹣1,0)![]()
(1)若x= ![]() ,求
,求 ![]() 与
与 ![]() 的夹角θ;
的夹角θ;
(2)若x∈[﹣ ![]() ,
, ![]() ],f(x)=λ
],f(x)=λ ![]()
![]() 的最大值为
的最大值为 ![]() ,求λ.
,求λ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则以下步骤可以得到函数f(x)的图象的是( ) 
A.将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向左平移 ![]() 个单位
个单位
B.将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向右平移 ![]() 个单位
个单位
C.将y=sinx的图象上的点纵坐标不变,横坐标变成原来的 ![]() ,然后再向右平移
,然后再向右平移 ![]() 个单位
个单位
D.将y=sinx的图象上的点纵坐标不变,横坐标变成原来的 ![]() ,然后再向左平移
,然后再向左平移 ![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com