
【题目】已知函数u(x)=xlnx,v(x)![]() x﹣1,m∈R.
x﹣1,m∈R.
(1)令m=2,求函数h(x)![]() 的单调区间;
的单调区间;
(2)令f(x)=u(x)﹣v(x),若函数f(x)恰有两个极值点x1,x2,且满足1![]() e(e为自然对数的底数)求x1x2的最大值.
e(e为自然对数的底数)求x1x2的最大值.
【答案】(1)单调递增区间是(0,e),单调递减区间是(e,+∞)(2)![]()
【解析】
(1)化简函数h(x)![]() ,求导,根据导数和函数的单调性的关系即可求出
,求导,根据导数和函数的单调性的关系即可求出
(2)函数f(x)恰有两个极值点x1,x2,则f′(x)=lnx﹣mx=0有两个正根,由此得到m(x2﹣x1)=lnx2﹣lnx1,m(x2+x1)=lnx2+lnx1,消参数m化简整理可得ln(x1x2)=ln![]()
![]() ,设t
,设t![]() ,构造函数g(t)=(
,构造函数g(t)=(![]() )lnt,利用导数判断函数的单调性,求出函数的最大值即可求出x1x2的最大值.
)lnt,利用导数判断函数的单调性,求出函数的最大值即可求出x1x2的最大值.
(1)令m=2,函数h(x)![]() ,∴h′(x)
,∴h′(x)![]() ,
,
令h′(x)=0,解得x=e,
∴当x∈(0,e)时,h′(x)>0,当x∈(e,+∞)时,h′(x)<0,
∴函数h(x)单调递增区间是(0,e),单调递减区间是(e,+∞)
(2)f(x)=u(x)﹣v(x)=xlnx![]() x+1,
x+1,
∴f′(x)=1+lnx﹣mx﹣1=lnx﹣mx,
∵函数f(x)恰有两个极值点x1,x2,
∴f′(x)=lnx﹣mx=0有两个不等正根,
∴lnx1﹣mx1=0,lnx2﹣mx2=0,
两式相减可得lnx2﹣lnx1=m(x2﹣x1),
两式相加可得m(x2+x1)=lnx2+lnx1,
∴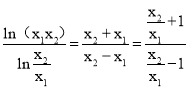
∴ln(x1x2)=ln![]()
![]() ,
,
设t![]() ,∵1
,∵1![]() e,∴1<t≤e,
e,∴1<t≤e,
设g(t)=(![]() )lnt,∴g′(t)
)lnt,∴g′(t)![]() ,
,
令φ(t)=t2﹣1﹣2tlnt,∴φ′(t)=2t﹣2(1+lnt)=2(t﹣1﹣lnt),
再令p(t)=t﹣1﹣lnt,∴p′(t)=1![]() 0恒成立,
0恒成立,
∴p(t)在(1,e]单调递增,∴φ′(t)=p(t)>p(1)=1﹣1﹣ln1=0,
∴φ(t)在(1,e]单调递增,∴g′(t)=φ(t)>φ(1)=1﹣1﹣2ln1=0,
∴g(t)在(1,e]单调递增,∴g(t)max=g(e)![]() ,
,
∴ln(x1x2)![]() ,∴x1x2
,∴x1x2![]()
故x1x2的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
, ![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学只有两位说的话是对的,则获得一等奖的作品是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设动点![]() 在圆
在圆![]() 上,动线段
上,动线段![]() 的中点
的中点![]() 的轨迹为
的轨迹为![]() ,
,![]() 与直线
与直线![]() 交点为
交点为![]() ,且直角坐标系中,
,且直角坐标系中,![]() 点的横坐标大于
点的横坐标大于![]() 点的横坐标,求点
点的横坐标,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:椭圆![]() 的顶点为
的顶点为![]() ,左右焦点分别为
,左右焦点分别为![]() ,
,![]() ,
,![]()
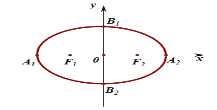
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试探究在
两点,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在求出点
为定值?若存在求出点![]() 的坐标,若不存在请说明理由?
的坐标,若不存在请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() :
:![]() 的焦点
的焦点![]() ,与抛物线
,与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() 的两条直线
的两条直线![]() 、
、![]() 分别交抛物线
分别交抛物线![]() 于点
于点![]() 、
、![]() 和
和![]() 、
、![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() 、
、![]() .如果直线
.如果直线![]() 与
与![]() 的斜率之积等于1,求证:直线
的斜率之积等于1,求证:直线![]() 经过一定点.
经过一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 参数方程为:
参数方程为:![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 参数方程为:
参数方程为:![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 交点分别为
交点分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,焦距为
,焦距为![]() ,点
,点![]() 为椭圆上一点,
为椭圆上一点,![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求椭圆的标准方程;
(2)设点![]() 为椭圆的上顶点,过椭圆内一点
为椭圆的上顶点,过椭圆内一点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,若
两点,若![]() 与
与![]() 的面积比为
的面积比为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
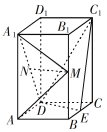
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com