
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.

(1)证明:AE⊥PD;
(2)若AB=2,PA=2,求二面角E-AF-C的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)已知可得![]() 为正三角形,由
为正三角形,由![]() 为
为![]() 的中点,得
的中点,得![]() ,可得
,可得![]() ,再由
,再由![]() 平面
平面![]() ,得
,得![]() ,由线面垂直的判定得
,由线面垂直的判定得![]() 平面
平面![]() ,从而可得结论;(2)由(1)知
,从而可得结论;(2)由(1)知 ![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图所示的空间直角坐标系.利用向量垂直数量积为零列方程求出平面
为坐标原点,建立如图所示的空间直角坐标系.利用向量垂直数量积为零列方程求出平面![]() 的法向量,结合
的法向量,结合![]() 为平面
为平面![]() 的一个法向量,利用空间向量夹角余弦公式可求出二面角
的一个法向量,利用空间向量夹角余弦公式可求出二面角![]() 的余弦值.
的余弦值.
(1)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.又BC∥AD,所以AE⊥AD.
因为PA⊥平面ABCD,AE平面ABCD,所以PA⊥AE.
又PA平面PAD,AD平面PAD,PA∩AD=A,
所以AE⊥平面PAD,所以AE⊥PD.
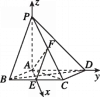
(2)由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系.由E,F分别为BC,PC的中点,易得A(0,0,0),B(![]() ,-1,0),D(0,2,0),E(
,-1,0),D(0,2,0),E(![]() ,0,0),F
,0,0),F![]() ,所以
,所以![]() =(
=(![]() ,0,0),
,0,0),![]() =
=![]() .设平面AEF的法向量为m=(x1,y1,z1),
.设平面AEF的法向量为m=(x1,y1,z1),
则![]() 即
即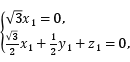
取z1=-1,则m=(0,2,-1).
连接BD.易知BD⊥AC,BD⊥PA,又PA∩AC=A,
所以BD⊥平面PAC,即BD⊥平面AFC,故![]() 为平面AFC的一个法向量,易得
为平面AFC的一个法向量,易得![]() =(-
=(-![]() ,3,0),
,3,0),
所以cos<m,![]() >=
>=![]() =
=![]() =
=![]() .
.
结合图形可知,所求二面角的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】环保部门对5家造纸厂进行排污检查,若检查不合格,则必须整改,整改后经复查仍然不合格的,则关闭.设每家造纸厂检查是否合格是相互独立的,且每家造纸厂检查前合格的概率是 ![]() ,整改后检查合格的概率是
,整改后检查合格的概率是 ![]() ,求:
,求:
(Ⅰ)恰好有两家造纸厂必须整改的概率;
(Ⅱ)至少要关闭一家造纸厂的概率;
(Ⅲ)平均多少家造纸厂需要整改?(其中( ![]() )5≈
)5≈ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥E-ABCD中,四边形ABCD是平行四边形,△BCE是等边三角形,△ABE是等腰直角三角形,∠BAE=90°,且AC=BC.

(1)证明:平面ABE⊥平面BCE;
(2)求二面角A-DE-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】8人围圆桌开会,其中正、副组长各1人,记录员1人.
(1)若正、副组长相邻而坐,有多少种坐法?
(2)若记录员坐于正、副组长之间,有多少种坐法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9这9个数字中取3个偶数和4个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)在(1)中的七位数中,偶数排在一起,奇数也排在一起的有多少个?
(3)在(1)中任意2个偶数都不相邻的七位数有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex﹣asinxcosx(a∈R,其中e是自然对数的底数).
(1)当a=0时,求f(x)的极值;
(2)若对于任意的x∈[0, ![]() ],f(x)≥0恒成立,求a的取值范围;
],f(x)≥0恒成立,求a的取值范围;
(3)是否存在实数a,使得函数f(x)在区间 ![]() 上有两个零点?若存在,求出a的取值范围;若不存在,请说明理由.
上有两个零点?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为万元. 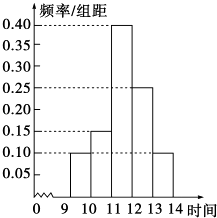
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,四点
,四点![]() 、
、![]() 、
、![]() 、
、![]() 中恰有三点在椭圆
中恰有三点在椭圆![]() 上。
上。
(1)求![]() 的方程:
的方程:
(2)椭圆![]() 上是否存在不同的两点
上是否存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称?若存在,请求出直线
对称?若存在,请求出直线![]() 的方程,若不存在,请说明理由;
的方程,若不存在,请说明理由;
(3)设直线![]() 不经过点
不经过点![]() 且与
且与![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率的和为1,求证:
的斜率的和为1,求证:![]() 过定点。
过定点。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正整数N除以正整数m后的余数为n,则记为N≡n(mod m),例如10≡4(mod 6).下面程序框图的算法源于我国古代闻名中外的(中国剩余定理),执行该程序框图,则输出的n等于( ) 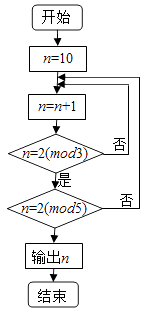
A.17
B.16
C.15
D.13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com