考点:空间中直线与直线之间的位置关系,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由C1D1∥B1A1,得∠B1A1M是异面直线A1M和C1D1所成角,由此能示出异面直线A1M和C1D1所成角的正切值.
(2)C1M=2时,由勾股定理得B1M⊥BM,A1M⊥BM,由此能证明BM⊥平面A1B1M.
解答:
(1)解:∵C
1D
1∥B
1A
1,
∴∠B
1A
1M是异面直线A
1M和C
1D
1所成角,
∵在长方体ABCD-A
1B
1C
1D
1中,A
1B
1⊥平面BCC
1B
1,
∴A
1B
1⊥B
1M,
∵AB=2,BC=2,CC
1=4,M为棱CC
1上一点,C
1M=1,
∴B
1M=
=
=
,
∴tan∠B
1A
1M=
=
,
∴异面直线A
1M和C
1D
1所成角的正切值为
.
(2)证明:C
1M=2时,B
1M=BM=
=2
,
∴
B1M2+BM2=
BB12,∴B
1M⊥BM.
∵
A1M2=A1C12+MC12=4+4+4=12,
A1B2=16+4=20,
∴
A1M2+BM2=
A1B2,
∴A
1M⊥BM,
又A
1M∩B
1M=M,∴BM⊥平面A
1B
1M.
点评:本题考查异面直线所成角的正切值的求法,考查直线与平面的证明,解题时要注意空间思维能力的培养.

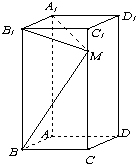 如图所示,在长方体ABCD-A1B1C1D1中,AB=2,BC=2,CC1=4,M为棱CC1上一点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=2,BC=2,CC1=4,M为棱CC1上一点.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案