
设各项均为正数的数列 的前n项和为Sn,已知
的前n项和为Sn,已知 ,且
,且 对一切
对一切 都成立.
都成立.
(1)若λ=1,求数列 的通项公式;
的通项公式;
(2)求λ的值,使数列 是等差数列.
是等差数列.
(1)an = 2n-1(2)λ = 0.
解析试题分析:(1)本题属于“已知 求
求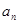 ”,利用
”,利用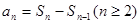 化简关系式. 因为
化简关系式. 因为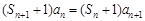 ,所以先分离
,所以先分离 与
与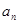 ,即
,即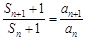 ,这是类等比,利用叠乘法得到
,这是类等比,利用叠乘法得到 ,再利用
,再利用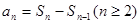 ,消去
,消去 得
得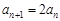 .求数列{an}通项公式时,需讨论当n = 1时是否满足
.求数列{an}通项公式时,需讨论当n = 1时是否满足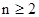 的情形.(2)解答本题需注意逻辑关系,由数列
的情形.(2)解答本题需注意逻辑关系,由数列 是等差数列得λ = 0,这是一个必要条件,还需验证其充分性,即λ = 0时,数列
是等差数列得λ = 0,这是一个必要条件,还需验证其充分性,即λ = 0时,数列 是等差数列.这可类似(1)的解答过程.
是等差数列.这可类似(1)的解答过程.
试题解析:解:(1)若λ = 1,则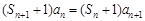 ,
,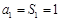 .
.
又∵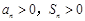 , ∴
, ∴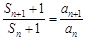 , 2分
, 2分
∴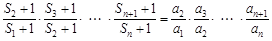 ,
,
化简,得 .①4分
.①4分
∴当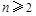 时,
时,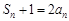 .②
.②
② -①,得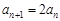 ,∴
,∴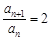 (
(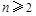 ).6分
).6分
∵当n = 1时, 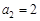 ,∴n = 1时上式也成立,
,∴n = 1时上式也成立,
∴数列{an}是首项为1,公比为2的等比数列, an = 2n-1( ).8分
).8分
(2)令n = 1,得 .令n = 2,得
.令n = 2,得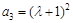 . 10分
. 10分
要使数列 是等差数列,必须有
是等差数列,必须有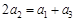 ,解得λ = 0. 11分
,解得λ = 0. 11分
当λ = 0时,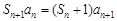 ,且
,且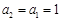 .
.
当n≥2时,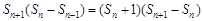 ,
,
整理,得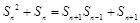 ,
,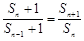 , 13分
, 13分
从而 ,
,
化简,得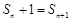 ,所以
,所以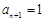 . 15分
. 15分
综上所述, (
( ),
),
所以λ = 0时,数列 是等差数列. 16分
是等差数列. 16分
考点:已知 求
求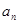


科目:高中数学 来源: 题型:解答题
已知数列 为等差数列,其公差d不为0,
为等差数列,其公差d不为0, 和
和 的等差中项为11,且
的等差中项为11,且 ,令
,令 ,数列
,数列 的前n项和为
的前n项和为 .
.
(1)求 及
及 ;
;
(2)是否存在正整数m,n(1<m<n),使得 成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
正实数数列{an}中,a1=1,a2=5,且{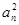 }成等差数列.
}成等差数列.
(1)证明:数列{an}中有无穷多项为无理数;
(2)当n为何值时,an为整数?并求出使an<200的所有整数项的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com