
分析 (1)求出函数的导数,计算f(1),f′(1),求出切线方程即可;
(2)令ϕ(x)=f(x)-(e-2)x-2=ex-x2-(e-2)x-1,则ϕ′(x)=ex-2x-(e-2),令t(x)=ϕ′(x),根据函数的单调性证明即可.
解答 解:(1)f′(x)=ex-2ax,f′(1)=e-2a,f(1)=e-a+1,
∴曲线y=f(x)在x=1处的切线方程为:
y-e+a-1=(e-2a)x-e+2a,
即:y=(e-2a)x+a+1,
由题意:e-2a=b,a+1=2,
∴a=1,b=e-2…(6分)
(2)证明:令ϕ(x)=f(x)-(e-2)x-2=ex-x2-(e-2)x-1,
则ϕ′(x)=ex-2x-(e-2),令t(x)=ϕ′(x),
则t′(x)=ex-2,
令t′(x)<0得:0<x<ln2 令t′(x)>0得:x>ln2,
∴t(x)=ϕ′(x)在(0,ln2)上单调递减,在(ln2,+∞)上单调递增
∵t(0)=ϕ′(0)=3-e>0,t(1)=ϕ′(1)=0,0<ln2<1,
∴t(ln2)=ϕ′(ln2)<0,
∴存在x0∈(0,1)使t(x0)=ϕ′(x0)=0,
且当x∈(0,x0)或x∈(1,+∞)时,t(x)=ϕ′(x)>0,
当x∈(x0,1)时,t(x)=ϕ′(x)<0,
∴ϕ(x)在(0,x0)上递增,在(x0,1)上递减,在上递增(1,+∞),
又ϕ(0)=ϕ(1)=0,所以有:ϕ(x)≥0,
即f(x)-(e-2)x-2≥0,
∴f(x)≥(e-2)x+2…(12分)
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
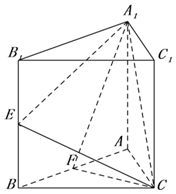 正三棱柱ABC-A1B1C1底边长为2,E,F分别为BB1,AB的中点.
正三棱柱ABC-A1B1C1底边长为2,E,F分别为BB1,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
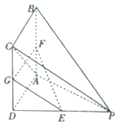 如图,四棱锥P-ABCD的底面ABCD是正方形,分E,F,G别为PD,AB,CD的中点,PD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是正方形,分E,F,G别为PD,AB,CD的中点,PD⊥平面ABCD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com