
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.
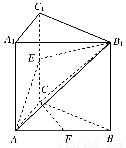
(1)求证:CF∥平面AB1E;
(2)求三棱锥C-AB1E在底面AB1E上的高.
(1)见解析(2)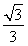
【解析】(1)证明:取AB1的中点G,连接EG,FG,

∵F、G分别是AB、AB1的中点,
∴FG∥BB1,FG=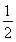 BB1.
BB1.
∵E为侧棱CC1的中点,
∴FG∥EC,FG=EC,
∴四边形FGEC是平行四边形,
∴CF∥EG,∵CF?平面AB1E,EG?平面AB1E,
∴CF∥平面AB1E.
(2)∵三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,
∴BB1⊥平面ABC.
又AC?平面ABC,∴AC⊥BB1,∵∠ACB=90°,∴AC⊥BC,
∵BB1∩BC=B,∴AC⊥平面EB1C,∴AC⊥CB1,
∴VA-EB1C=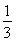 S△EB1C·AC
S△EB1C·AC
=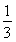 ×
×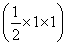 ×1=
×1= .
.
∵AE=EB1=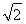 ,AB1=
,AB1=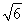 ,∴S△AB1E=
,∴S△AB1E= ,
,
∵VC-AB1E=VA-EB1C,∴三棱锥C-AB1E在底面AB1E上的高为 .
.


科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:选择题
已知i是虚数单位,复数z的共轭复数是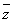 ,如果|z|+
,如果|z|+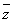 =8-4i,那么z等于( )
=8-4i,那么z等于( )
A.-3-4i B.-3+4i
C.4+3i D.3+4i
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:选择题
连续抛掷两枚正方体骰子(它们的六个面分别标有数字1,2,3,4,5,6),记所得朝上的面的点数分别为x,y,过坐标原点和点P(x,y)的直线的倾斜角为θ,则θ>60°的概率为( )
A.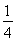 B.
B.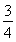 C.
C.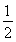 D.
D.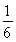
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
过双曲线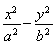 =1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=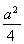 的切线,交双曲线右支于点P,切点为E,若
的切线,交双曲线右支于点P,切点为E,若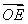 =
=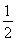 (
(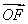 +
+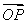 ),则双曲线的离心率为( )
),则双曲线的离心率为( )
A. 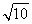 B.
B. 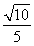 C.
C. 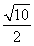 D.
D.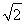
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( )
A.相切 B.相交
C.相离 D.不确定
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:填空题
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于点O,剪去△AOB,将剩余部分沿OC,OD折叠,使OA,OB重合,则以A,B,C,D,O为顶点的四面体的体积为________.
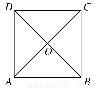
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:选择题
设m,n是两条不同的直线,α,β,γ是三个不同的平面,有以下四个命题:
①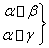 ⇒β∥γ②
⇒β∥γ②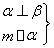 ⇒m⊥β③
⇒m⊥β③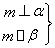 ⇒α⊥β④
⇒α⊥β④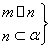 ⇒m∥α
⇒m∥α
其中正确的命题是( )
A.①④ B.②③ C.①③ D.②④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:选择题
已知数列{an},{bn}满足a1=b1=3,an+1-an=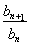 =3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
=3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
A.92 012 B.272 012 C.92 013 D.272 013
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
已知函数y=f(x)的图象关于y轴对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,a=(20.2)·f(20.2),b=(logπ3)·f(logπ3),c=(log39)·f(log39),则a,b,c的大小关系是( )
A.b>a>c B.c>a>b
C.c>b>a D.a>c>b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com