
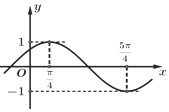
 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.分析 (Ⅰ)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,可得h(x)的解析式,再根据h′(x)≥0恒成立,求得a的范围.
解答 解:(Ⅰ)根据函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象,
可得A=1,$\frac{T}{2}$=$\frac{5π}{4}$-$\frac{π}{4}$=$\frac{π}{ω}$,∴ω=1.
再根据五点法作图可得1•$\frac{π}{4}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{4}$,∴f(x)=sin(x+$\frac{π}{4}$).
(Ⅱ)把函数y=f(x)的图象向右平移$\frac{π}{4}$个单位后得到函数g(x)=sin(x-$\frac{π}{4}$+$\frac{π}{4}$)=sinx的图象
函数$h(x)=ax+\frac{1}{2}g(2x)-g(x)$=ax+$\frac{1}{2}$sin2x-sinx 在(-∞,+∞)单调递增,
∴h′(x)=a+cos2x-cosx=2cos2x-cosx-1+a=2${(cosx-\frac{1}{4})}^{2}$-$\frac{9}{8}$+a≥0恒成立,
∴-$\frac{9}{8}$+a≥0恒成立,即a≥$\frac{9}{8}$恒成立,故a的范围为[$\frac{9}{8}$,+∞).
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值.还考查了函数y=Asin(ωx+φ)的图象变换规律,利用导数研究函数的单调性,函数的恒成立问题,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{a=-1}\\{b=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=0}\\{b=-1}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最大值为$3+\frac{1}{e}$ | B. | 函数f(x)的最小值为$3+\frac{1}{e}$ | ||
| C. | 函数f(x)的最大值为3 | D. | 函数f(x)的最小值为3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 1 | 3 | 5 | 7 | |
| 15 | 13 | 11 | 9 | |
| 17 | 19 | 21 | 23 | |
| 31 | 29 | 27 | 25 | |
| … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x≥0,x2+x-1<0”的否定是“?x<0,x2+x-1<0” | |
| C. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com