
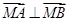 ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
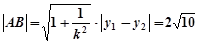 .(2)
.(2)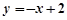 .
.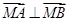 ,把此条件用坐标表示出来,借助韦达定理建立关于k的方程,求出k值,再验证是否满足判别式大于零
,把此条件用坐标表示出来,借助韦达定理建立关于k的方程,求出k值,再验证是否满足判别式大于零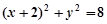 ,所以圆心N为(-2,0),半径
,所以圆心N为(-2,0),半径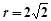 ,
,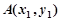 ,
,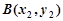 ,
,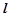 的斜率为1时,设
的斜率为1时,设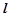 的方程为
的方程为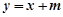 即
即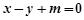 ,因为直线
,因为直线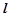 是圆N的切线,所以
是圆N的切线,所以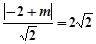 ,解得
,解得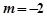 或
或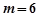 (舍去)
(舍去)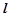 的方程为
的方程为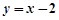 , ………………3分
, ………………3分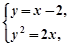 消去
消去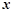 得
得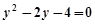 ,所以
,所以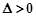 ,
,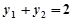 ,
,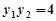 ,
,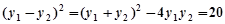
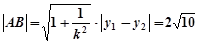 .……………………6分
.……………………6分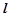 的方程为
的方程为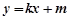 即
即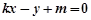 (
(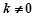 ),
),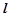 是圆N的切线,所以
是圆N的切线,所以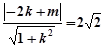 ,
,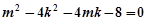 ①………………8分
①………………8分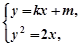 消去
消去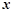 得
得 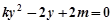 ,
,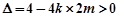 即
即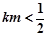 且
且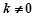 ,
, 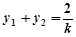 ,
,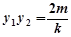 .
.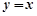 对称,所以点M为
对称,所以点M为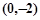
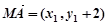 ,
,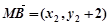 ,
, 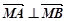 ,所以
,所以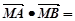
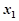
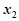 +
+ 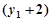
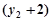
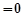 ,……9分
,……9分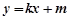 上代入化简得,
上代入化简得,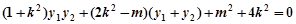 .
.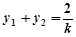 ,
,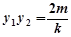 得
得 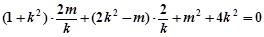
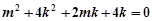 ………②
………②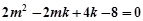
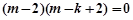 ,解得
,解得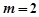 或
或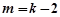
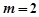 时,代入①解得
时,代入①解得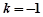 ,满足条件
,满足条件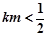 且
且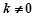 ,
,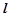 的方程为
的方程为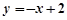 ;
;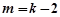 时,代入①整理得
时,代入①整理得 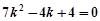 ,无解.………………11分
,无解.………………11分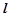 的斜率不存在时,因为直线
的斜率不存在时,因为直线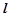 是圆N的切线,所以
是圆N的切线,所以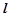 的方程为
的方程为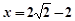 ,则得
,则得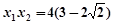 ,
,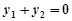 ,
,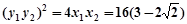 即
即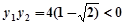
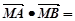
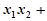
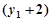
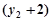
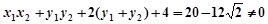
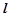 的斜率不存在时
的斜率不存在时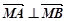 不成立.
不成立.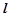 ,其方程为
,其方程为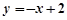 .
.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com