
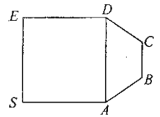
【题目】某产品的包装纸可类比如图所示的平面图形,其可看作是由正方形![]() 和等腰梯形
和等腰梯形![]() 拼成,已知
拼成,已知![]() ,
,![]() ,在包装的过程中,沿着
,在包装的过程中,沿着![]() 将正方形
将正方形![]() 折起,直至
折起,直至![]() ,得到多面体
,得到多面体![]() ,
,![]() 分别为
分别为![]() 中点.
中点.
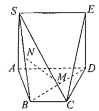
(1)证明:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】为丰富学生课外生活,某市组织了高中生钢笔书法比赛,比赛分两个阶段进行:第一阶段由评委给出所有参赛作品评分,并确定优胜者;第二阶段为附加赛,参赛人员由组委会按规则另行确定.数据统计员对第一阶段的分数进行了统计分析,这些分数![]() 都在
都在![]() 内,在以组距为5画分数的频率分布直方图(设“
内,在以组距为5画分数的频率分布直方图(设“![]() ”)时,发现
”)时,发现![]() 满足
满足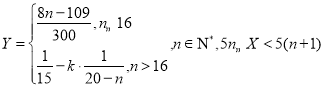 .
.
(1)试确定![]() 的所有取值,并求
的所有取值,并求![]() ;
;
(2)组委会确定:在第一阶段比赛中低于85分的参赛者无缘获奖也不能参加附加赛;分数在![]() 的参赛者评为一等奖;分数在
的参赛者评为一等奖;分数在![]() 的同学评为二等奖,但通过附加赛有
的同学评为二等奖,但通过附加赛有![]() 的概率提升为一等奖;分数在
的概率提升为一等奖;分数在![]() 的同学评为三等奖,但通过附加赛有
的同学评为三等奖,但通过附加赛有![]() 的概率提升为二等奖(所有参加附加赛的获奖人员均不降低获奖等级).已知学生
的概率提升为二等奖(所有参加附加赛的获奖人员均不降低获奖等级).已知学生![]() 和
和![]() 均参加了本次比赛,且学生
均参加了本次比赛,且学生![]() 在第一阶段评为二等奖.
在第一阶段评为二等奖.
(![]() )求学生
)求学生![]() 最终获奖等级不低于学生
最终获奖等级不低于学生![]() 的最终获奖等级的概率;
的最终获奖等级的概率;
(![]() )已知学生
)已知学生![]() 和
和![]() 都获奖,记
都获奖,记![]() 两位同学最终获得一等奖的人数为
两位同学最终获得一等奖的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某传染病疫情爆发期间,当地政府积极整合医疗资源,建立“舱医院”对所有密切接触者进行14天的隔离观察治疗.治疗期满后若检测指标仍未达到合格标准,则转入指定专科医院做进一步的治疗.“舱医院”对所有人员在“入口”及“出口”时都进行了医学指标检测,若“入口”检测指标在35以下者则不需进入“舱医院”而是直接进入指定专科医院进行治疗.以下是20名进入“舱医院”的密切接触者的“入口”及“出口”医学检测指标:
入口 | 50 | 35 | 35 | 40 | 55 | 90 | 80 | 60 | 60 | 60 | 65 | 35 | 60 | 90 | 35 | 40 | 55 | 50 | 65 | 50 |
出口 | 70 | 50 | 60 | 50 | 75 | 70 | 85 | 70 | 80 | 70 | 55 | 50 | 75 | 90 | 60 | 60 | 65 | 70 | 75 | 70 |
(Ⅰ)建立![]() 关于
关于![]() 的回归方程;(回归方程的系数精确到0.1)
的回归方程;(回归方程的系数精确到0.1)
(Ⅱ)如果60是“舱医院”的“出口”最低合格指标,那么,“入口”指标低于多少时,将来这些密切接触者将不能进入“舱医院”而是直接进入指定专科医院接受治疗.(检测指标为整数)
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: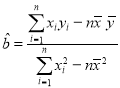 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省级示范高中高三年级对各科考试的评价指标中,有“难度系数“和“区分度“两个指标中,难度系数![]() ,区分度
,区分度![]() .
.
(1)某次数学考试(满分为150分),随机从实验班和普通班各抽取三人,实验班三人的成绩分别为147,142,137;普通班三人的成绩分别为97,102,113.通过样本估计本次考试的区分度(精确0.01).
(2)如表表格是该校高三年级6次数学考试的统计数据:
难度系数x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
区分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①计算相关系数r,|r|<0.75时,认为相关性弱;|r|≥0.75时,认为相关性强.通过计算说明,能否利用线性回归模型描述y与x的关系(精确到0.01).
②ti=|xi﹣0.74|(i=1,2,…,6),求出y关于t的线性回归方程,并预测x=0.75时y的值(精确到0.01).
附注:参考数据: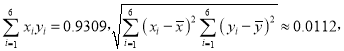
![]()
![]()
参考公式:相关系数 r,回归直线
r,回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,求
两点,求![]() 的最大值,并求
的最大值,并求![]() 取得最大值时直线
取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆节期间,滕州市实验小学举行了一次科普知识竞赛活动,设置了一等奖、二等奖、三等奖、四等奖及纪念奖,获奖人数的分配情况如图所示,各个奖品的单价分别为:一等奖50元、二等奖20元、三等奖10元,四等奖5元,纪念奖2元,则以下说法中不正确的是( )
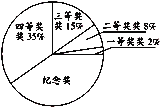
A.获纪念奖的人数最多B.各个奖项中二等奖的总费用最高
C.购买奖品的费用平均数为6.65元D.购买奖品的费用中位数为5元
查看答案和解析>>
科目:高中数学 来源: 题型:
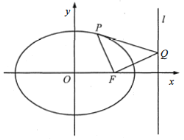
【题目】如图,在平面直角坐标系![]() 中,己知
中,己知![]() 是椭圆
是椭圆![]() 的右焦点,
的右焦点,![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的任意一点,过
轴上方的任意一点,过![]() 作垂直于
作垂直于![]() 的直线交其右准线
的直线交其右准线![]() 于点
于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求证:直线
,求证:直线![]() 与椭圆
与椭圆![]() 相切;
相切;
(3)在椭圆![]() 上是否存在点
上是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,求出所有符合条件的点
是平行四边形?若存在,求出所有符合条件的点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com