
【题目】设函数f(x)=|2x+1|-|x-4|.
(1)解不等式f(x)>2;
(2)若函数f(x)≥m恒成立,求m的最大整数值.
【答案】(1)见解析;(2)1;(3)![]() .
.
【解析】试题分析:
(1)利用绝对值的定义去绝对值符号,化函数为分段函数形式,然后分段解不等式可得结论,也可作出函数![]() 的图象与直线
的图象与直线![]() ,从图象观察出不等式的解;
,从图象观察出不等式的解;
(2)作出函数![]() 图象可求得
图象可求得![]() 的最小值,从而可得
的最小值,从而可得![]() 的范围,在其中取最大整数
的范围,在其中取最大整数
试题解析:
(1)令y=|2x+1|-|x-4|,则
y=
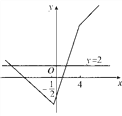
作出函数y=|2x+1|-|x-4|的图像,它与直线y=2的交点为(-7,2)和(![]() ,2).
,2).
所以|2x+1|-|x-4|>2的解集为(-∞,-7)∪(![]() ,+∞).
,+∞).
(2)由函数y=|2x+1|-|x-4|的图像可知,当x=-![]() 时,y=|2x+1|-|x-4|取得最小值-
时,y=|2x+1|-|x-4|取得最小值-![]() . 由题m<=-9/2,故m的最大整数值-5.
. 由题m<=-9/2,故m的最大整数值-5.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;
(2)设![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。
的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。
⑴ 求![]() ,
, ![]() 的值;
的值;
⑵ 直接写出![]() 时,
时, ![]() 的取值范围。
的取值范围。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=
的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=![]() ,
,
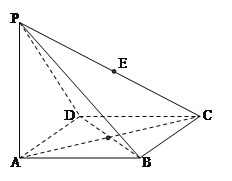
(1)求证:平面PBD⊥平面PAC;
(2)求三棱锥P--BDC的体积。
(3)在线段PC上是否存在一点E,使PC⊥平面EBD成立.如果存在,求出EC的长;如果不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() )的图像关于坐标原点对称。
)的图像关于坐标原点对称。
(1)求![]() 的值,并求出函数
的值,并求出函数![]() 的零点;
的零点;
(2)若函数![]() 在
在![]() 内存在零点,求实数
内存在零点,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求满足条件的最小整数
上恒成立,求满足条件的最小整数![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
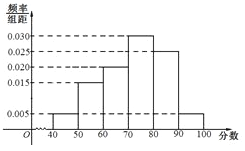
【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)假设抽出学生的数学成绩在![]() 段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为
段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数![]() 在定义域内给定区间
在定义域内给定区间![]() 上存在
上存在![]() (
(![]() ),满足
),满足![]() ,则称函数
,则称函数![]() 是
是![]() 上的“平均值函数”,
上的“平均值函数”, ![]() 是它的一个均值点.如
是它的一个均值点.如![]() 是
是![]() 上的平均值函数,0就是他的均值点.
上的平均值函数,0就是他的均值点.
(1)判断函数![]() 在区间
在区间![]() 上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
(2)若函数![]() 是区间
是区间![]() 上的平均值函数,试确定实数
上的平均值函数,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=1,AD=![]() 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
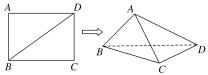
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com