
【题目】设![]() 为任意给定的质数.证明:一定存在质数
为任意给定的质数.证明:一定存在质数![]() ,使得对任意的整数
,使得对任意的整数![]() ,数
,数![]() 都不能被
都不能被![]() 整除.
整除.
【答案】见解析
【解析】
要找的质数![]() 仅和
仅和![]() 有关,与
有关,与![]() 无关,所以,对任意的正整数
无关,所以,对任意的正整数![]() ,若
,若![]() 则
则![]() .也就是说,若
.也就是说,若![]() ,则
,则![]() .
.
这样,问题就转化为选取适当的![]() ,代替
,代替![]() 来讨论
来讨论![]() .
.
最简单的选择是取![]() .先对此进行试探性讨论.有
.先对此进行试探性讨论.有
![]() .
.
如果找到![]() 的质因数
的质因数![]() ,能使得对任意的整数
,能使得对任意的整数![]() ,
,![]() 都不能被
都不能被![]() 整除,那么,就解决了本题.
整除,那么,就解决了本题.
对![]() 的质因数
的质因数![]() ,
,![]() 可分为两类:
可分为两类:
(1)![]() 不能被
不能被![]() 整除.对这些
整除.对这些![]() 就有
就有![]() ,因而,
,因而,![]() .
.
(2)![]() 被
被![]() 整除.此时,希望对所选取的
整除.此时,希望对所选取的![]() 的质因数
的质因数![]() 加上进一步可实现的条件,能有
加上进一步可实现的条件,能有![]() .
.
假定这样的![]() 存在,取质数
存在,取质数![]() .若存在某个
.若存在某个![]() ,使得
,使得![]() ,则
,则![]() .由此及
.由此及![]() 推出
推出![]() .其中,
.其中,![]() .
.
注意到![]() ,
,![]() ,或
,或![]() .
.
如果取得到质数![]() ,使得
,使得![]() ,即
,即![]() ,则必有
,则必有![]() .
.
如果再要求![]() ,则有
,则有
![]() .
.
这就满足本题的要求.
由以上分析知,只要存在质数q满足条件:
(i)![]() .,(ii)
.,(ii)![]() ,及(iii)
,及(iii)![]() .这样的质数
.这样的质数![]() 就满足本题的要求.
就满足本题的要求.
下面具体来找这样的质数![]() .
.
由前两个条件启发,考虑
![]() 的质因数
的质因数![]() .
.
显见,这样的![]() 不等于
不等于![]() .
.
若![]() ,则由此及
,则由此及
![]() ,
,
推出![]() .矛盾.
.矛盾.
所以,![]() 满足条件(i)和(ii).
满足条件(i)和(ii).
又![]() ,
,
所以,![]() 必有一个质因数
必有一个质因数![]() ,使得
,使得![]() ,即这样的
,即这样的![]() 满足条件(iii).
满足条件(iii).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在正方体的8个顶点、12条棱的中点、6个侧面的中心点、1个体的中心点,这27个点中,共球面的8点组的个数是().
A. 4462 B. 4584 C. 4590 D. 4602
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券2张,每张可获价值50元的奖品;有二等奖券2张,每张可获价值10元的奖品;其余6张没有奖.某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X元的概率分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在地面上同一地点观测远方匀速垂直上升的热气球,在上午10点整热气球的仰角是![]() ,到上午10点20分的仰角变成
,到上午10点20分的仰角变成![]() .请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数( )
.请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数( )
|
|
|
|
|
|
|
|
|
|
| 0.5 | 0.559 | 0.629 | 0.643 | 0.656 | 0.669 | 0.682 | 0.695 | 0.707 |
| 0.866 | 0.829 | 0.777 | 0.766 | 0.755 | 0.743 | 0.731 | 0.719 | 0.707 |
| 0.577 | 0.675 | 0.810 | 0.839 | 0.869 | 0.900 | 0.933 | 0.966 | 1.0 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“难度系数”反映试题的难易程度,难度系数越大,题目得分率越高,难度也就越小.“难度系数”的计算公式为![]() ,其中,
,其中,![]() 为难度系数,
为难度系数,![]() 为样本平均失分,
为样本平均失分,![]() 为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度系数 | 0.7 | 0.64 | 0.6 | 0.6 | 0.55 |
测试后,随机抽取了50名学生的数据进行统计,结果如下:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
实测平均分 | 102 | 99 | 93 | 93 | 87 |
(1)根据试卷2的难度系数估计这480名学生第2套试卷的平均分;
(2)从抽样的50名学生的5套试卷中随机抽取2套试卷,记这2套试卷中平均分超过96分的套数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)试卷的预估难度系数和实测难度系数之间会有偏差.设![]() 为第
为第![]() 套试卷的实测难度系数,并定义统计量
套试卷的实测难度系数,并定义统计量![]() ,若
,若![]() ,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.
,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx与g(x)=log4(a2x﹣![]() a),其中f(x)是偶函数.
a),其中f(x)是偶函数.
(1)求实数k的值;
(2)求函数g(x)的定义域;
(3)若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定一个四面体,若存在一个侧面(其所在平面为![]() ),使得在将其余三个侧面分别绕其位于平面
),使得在将其余三个侧面分别绕其位于平面![]() 上的边向体外方向旋转至平面
上的边向体外方向旋转至平面![]() 上时,四个侧面在平面
上时,四个侧面在平面![]() 上共同组成的图形恰好是一个三角形,则称该四面体是一个“平展四面体”.若有一个平展四面体,它的一个侧面的三边长为a、b、c,试确定a、b、c的关系,并求该四面体的体积(用a、b、c表示).
上共同组成的图形恰好是一个三角形,则称该四面体是一个“平展四面体”.若有一个平展四面体,它的一个侧面的三边长为a、b、c,试确定a、b、c的关系,并求该四面体的体积(用a、b、c表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
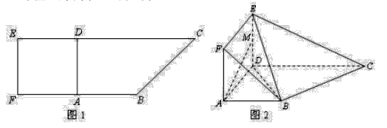
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向外作正方形
为一边向外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com