练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知△ABC内一点O满足 = ，若△ABC内任意投一个点，则该点△OAC内的概率为（ ）
    A.
    B.
    C.
    D.

    【答案】C
    【解析】解：以 ， 为邻边作平行四边形OBDC，则 + =
    ∵ = ，
    ∴3 = ，
    作AB的两个三等分点E，F，则 = = ，
    ∴O到AC的距离是E到AC距离的一半，B到AC的距离是O到AC距离的3倍，如图
    ∴S△AOC= S△ABC ．
    故△ABC内任意投一个点，则该点△OAC内的概率为 ，
    故选：C．

    【考点精析】本题主要考查了几何概型的相关知识点，需要掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在三棱锥P﹣ABC中，D为AB的中点．

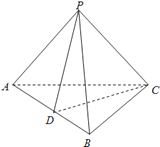
    （1）与BC平行的平面PDE交AC于点E，判断点E在AC上的位置并说明理由如下：

    （2）若PA=PB，且△PCD为锐角三角形，又平面PCD⊥平面ABC，求证：AB⊥PC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某次测验中，有6位同学的平均成绩为75分．用xn表示编号为n（n=1，2，…，6）的同学所得成绩，且前5位同学同学的成绩如表：

    n

    1

    2

    3

    4

    5

    x0

    70

    76

    72

    70

    72


    （1）求第6位同学的成绩x6及这6位同学成绩的标准差s；
    （2）若从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间[68，75）中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市教育部门拟从18名高中数学教师中选拔2人参加省教师技能大赛．为缩短比赛时间，将这18名教师随机分成， 两组，其选拔赛成绩的茎叶图如图所示．该教育部门先将成绩不低于85分的教师初选出来进行培训后，再从中选拔2人参加省教师技能大赛．

    （Ⅰ）若仅从初选选手中随机抽选2人参加省赛，并记抽选的2人中来自组的人数为，试求的分布列和期望值；

    （Ⅱ）在（Ⅰ）的条件下，若参加省赛的2人是同性的概率等于，求初选出来参加培训的男教师和女教师的人数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知PA垂直于矩形ABCD所在的平面，M，N分别是AB，PC的中点，若∠PDA=45°，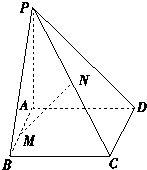
    （1）求证：MN∥平面PAD且MN⊥平面PCD．
    （2）探究矩形ABCD满足什么条件时，有PC⊥BD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（3，﹣4）， =（6，﹣3）， =（5﹣x，﹣3﹣y）， =（4，1）
    （1）若四边形ABCD是平行四边形，求x，y的值；
    （2）若△ABC为等腰直角三角形，且∠B为直角，求x，y的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】探究函数的最小值，并确定取得最小值时x的值.列表如下：

    x

    …

    0.5

    1

    1.5

    1.7

    1.9

    2

    2.1

    2.2

    2.3

    3

    4

    5

    7

    …

    y

    …

    8.5

    5

    4.17

    4.05

    4.005

    4

    4.005

    4.002

    4.04

    4.3

    5

    4.8

    7.57

    …

    请观察表中y值随x值变化的特点，完成以下的问题.

    函数在区间（0，2）上递减；

    函数在区间 上递增.

    当 时， .

    证明：函数在区间（0，2）递减.

    思考：函数时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设两条直线的方程分别为x+y+a=0和 x+y+b=0，已知a、b是关于x的方程x2+x+c=0的两个实根，且0≤c≤ ，则这两条直线间距离的最大值和最小值分别为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某电影院共有1000个座位，票价不分等次，根据影院的经营经验，当每张票价不超过10元时，票可全售出；当每张票价高于10元时，每提高1元，将有30张票不能售出，为了获得更好的收益，需给影院定一个合适的票价，需符合的基本条件是：①为了方便找零和算账，票价定为1元的整数倍；②电影院放一场电影的成本费用支出为5750元，票房的收入必须高于成本支出，用x（元）表示每张票价，用y（元）表示该影院放映一场的净收入（除去成本费用支出后的收入）
    问：
    （1）把y表示为x的函数，并求其定义域；
    （2）试问在符合基本条件的前提下，票价定为多少时，放映一场的净收人最多？

    查看答案和解析>>

    同步练习册答案