
【题目】已知椭圆![]() :
:![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,直线
,直线
![]() 与椭圆
与椭圆![]() 的两个交点间的距离为
的两个交点间的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,过![]() ,
,![]() 作两条平行线
作两条平行线![]() ,
,![]() 与椭圆
与椭圆![]() 的上半部分分别交于
的上半部分分别交于![]() ,
,![]() 两点,求四边形
两点,求四边形
![]() 面积的最大值.
面积的最大值.

科目:高中数学 来源: 题型:
【题目】给出下列四个说法:
①命题“![]() ,都有
,都有![]() ”的否定是“
”的否定是“![]() ,使得
,使得![]() ”;
”;
②已知![]() 、
、![]() ,命题“若
,命题“若![]() ,则
,则![]() ”的逆否命题是真命题;
”的逆否命题是真命题;
③![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
④若![]() 为函数
为函数![]() 的零点,则
的零点,则![]() .
.
其中正确的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.

(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的准线与
的准线与![]() 轴的交点为
轴的交点为![]() ,过
,过![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() 两点.
两点.
(1)求线段![]() 中点的轨迹;
中点的轨迹;
(2)若线段![]() 的垂直平分线交对称轴于
的垂直平分线交对称轴于![]() ),求
),求![]() 的取值范围;
的取值范围;
(3)若直线的斜率依次取![]() 时,线段
时,线段![]() 的垂直平分线与对称轴的交点依次为
的垂直平分线与对称轴的交点依次为
![]() ,当
,当![]() 时,
时,
求:![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图点![]() 是半径为
是半径为![]() 的砂轮边缘上的一个质点,它从初始位置
的砂轮边缘上的一个质点,它从初始位置![]() (
(![]() ,
,![]() )开始,按逆时针方向每
)开始,按逆时针方向每![]() 旋转一周,
旋转一周,![]() .
.
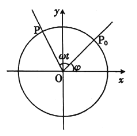
(1)求点![]() 的纵坐标
的纵坐标![]() 关于时间
关于时间![]() 的函数关系;
的函数关系;
(2)求点![]() 的运动周期和频率;
的运动周期和频率;
(3)函数![]() 的图像可由余弦曲线经过怎样的变化得到?
的图像可由余弦曲线经过怎样的变化得到?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com