
【题目】已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)若椭圆的离心率为![]() ,焦距为2,求线段
,焦距为2,求线段![]() 的长;
的长;
(2)若向量![]() 与向量
与向量![]() 互相垂直(其中
互相垂直(其中![]() 为坐标原点),当椭圆的离心率
为坐标原点),当椭圆的离心率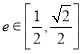 时,求椭圆的长轴长的最大值.
时,求椭圆的长轴长的最大值.
科目:高中数学 来源: 题型:
【题目】随着计算机的出现,图标被赋予了新的含义,又有了新的用武之地.在计算机应用领域,图标成了具有明确指代含义的计算机图形.如图所示的图标是一种被称之为“黑白太阳”的图标,该图标共分为3部分.第一部分为外部的八个全等的矩形,每一个矩形的长为3、宽为1;第二部分为圆环部分,大圆半径为3,小圆半径为2;第三部分为圆环内部的白色区域.在整个“黑白太阳”图标中随机取一点,则此点取自图标第三部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程是:
的极坐标方程是:![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程.
的直角坐标方程.
(2)点![]() 是曲线
是曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值与最小值.
距离的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com