
【题目】已知函数![]() ,
,![]()
(1)写出函数![]() 的解析式;
的解析式;
(2)若直线![]() 与曲线
与曲线![]() 有三个不同的交点,求
有三个不同的交点,求![]() 的取值范围;
的取值范围;
(3)若直线 ![]() 与曲线
与曲线![]() 在
在![]() 内有交点,求
内有交点,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]()
![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)先分类讨论求出|f(x)|的解析式,即得函数![]() 的解析式;(2)当
的解析式;(2)当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 只有2个交点,不符题意.当
只有2个交点,不符题意.当![]() 时,由题意得,直线
时,由题意得,直线![]() 与曲线
与曲线![]() 在
在![]() 或
或![]() 内必有一个交点,且在
内必有一个交点,且在![]() 的范围内有两个交点.由
的范围内有两个交点.由![]() 消去
消去![]() 得
得![]() .令
.令![]() ,写出
,写出![]() 应满足条件解得;(3)由方程组
应满足条件解得;(3)由方程组![]() 消去
消去![]() 得
得![]() .由题意知方程在
.由题意知方程在![]() ,
,![]() 内至少有一个实根,设两根为
内至少有一个实根,设两根为![]() ,
,![]() ,不妨设
,不妨设![]() ,
,![]() ,
,![]() .由根与系数关系得
.由根与系数关系得![]() ,
,![]() .代入
.代入![]() 求解即可.
求解即可.
(1)当![]() ,得
,得![]() 或
或![]() ,此时
,此时![]() ;
;
当![]() ,得
,得![]() ,此时
,此时![]()
∴![]()
![]()
(2)当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 只有2个交点,不符题意.
只有2个交点,不符题意.
当![]() 时,由题意得,直线
时,由题意得,直线![]() 与曲线
与曲线![]() 在
在![]() 或
或![]() 内必有一个交点,且在
内必有一个交点,且在![]() 的范围内有两个交点.
的范围内有两个交点.
由![]() ,消去
,消去![]() 得
得![]() .
.
令![]() ,则
,则![]() 应同时满足以下条件:
应同时满足以下条件:
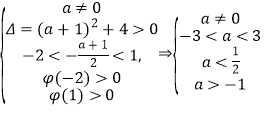 ,
,
解得![]() 或
或![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]()
(3)由方程组![]() ,消去
,消去![]() 得
得![]() .
.
由题意知方程在![]() 内至少有一个实根,设两根为
内至少有一个实根,设两根为![]() ,
,
不妨设![]() ,
,![]() ,由根与系数关系得
,由根与系数关系得![]() ,
,![]()
∴![]()
![]()
![]()
![]()
当且仅当![]() 时取等.
时取等.
所以![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)上的函数 f(x),对于任意正实数 a、b,都有 f(ab)=f(a)+f(b)﹣1,f(2)=0,且当 x>1 时,f(x)<1.
(1)求 f(1)及![]() 的值;
的值;
(2)求证:f(x)在(0,+∞)上是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x)=f(2-x),且f(1)=6,f(3)=2.
(1)求f(x)的解析式
(2)是否存在实数m,使得在[-1,3]上f(x)的图象恒在直线y=2mx+1的上方?若存在,求m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣ln(1﹣x),给出以下四个命题: ①x∈(﹣1,1),有f(﹣x)=﹣f(x);
②x1 , x2∈(﹣1,1)且x1≠x2 , 有 ![]() ;
;
③x1 , x2∈(0,1),有 ![]() ;
;
④x∈(﹣1,1),|f(x)|≥2|x|.
其中所有真命题的序号是( )
A.①②
B.③④
C.①②③
D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图: 
(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求计算出具体值,给出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此2×2列联表,并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关;
A | B | 合计 | |
认可 | |||
不认可 | |||
合计 |
(Ⅲ)若从此样本中的A城市和B城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自B城市的概率是多少?
附:参考数据:
(参考公式: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正实数a,b,c,函数f(x)=|x+a||x+b|. (Ⅰ)若a=1,b=3,解关于x的不等式f(x)+x+1<0;
(Ⅱ)求证:f(1)f(c)≥16abc.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC. 
(Ⅰ)求证:AC⊥BE;
(Ⅱ)若二面角E﹣BA﹣D的余弦值为 ![]() ,求三棱锥A﹣BCD的体积.
,求三棱锥A﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 ![]() . (I)求曲线C2的直角坐标系方程;
. (I)求曲线C2的直角坐标系方程;
(II)设M1是曲线C1上的点,M2是曲线C2上的点,求|M1M2|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com