Question

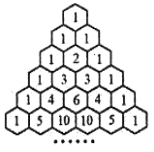
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，即杨辉三角，这是数学史上的一个伟大成就.在“杨辉三角”中，已知第行的所有数字之和为，若去除所有为1的项，依次构成数列2，3，3，4，6，4，5，10，10，5，……，则此数列的前56项和为（ ）

A. 2060B. 2038C. 4084D. 4108

Answer 1

【答案】C

【解析】

利用n次二项式系数对应杨辉三角形的第行，然后令得到对应项的系数和，结合等比数列和等差数列的公式进行转化求解即可.

n次二项式系数对应杨辉三角形的第行，

例如，系数分别为1,2,1，对应杨辉三角形的第3行，

令，就可以求出该行的系数之和，

第1行为，第2行为，第3行为，以此类推，

即每一行数字和为首项为1，公比为2的等比数列.

则杨辉三角形的前n项和为

若去除所有的为1的项，则剩下的每一行的个数为1,2,3,4,…,可以看成构成一个首项为1，公差为1的等差数列，则，可得当，去除两端“1”可得，则此数列前55项和为，所以第56项为第13行去除1的第一个数,所以该数列前56项和为，故选C.