
【题目】已知△ABC的三个内角A,B,C所对的边分别是a,b,c,向量![]() =(cos B,cos C),
=(cos B,cos C),![]() =(2a+c,b),且
=(2a+c,b),且![]() ⊥
⊥![]() .
.
(1)求角B的大小;
(2)若b=![]() ,求a+c的范围.
,求a+c的范围.
【答案】(1)![]() (2)(
(2)(![]() ,2].
,2].
【解析】
(1)利用平面向量的数量积运算法则列出关系式,利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式化简,求出cosB的值,即可确定出B的度数;
(2)由b及cosB的值,利用余弦定理列出关系式,再利用基本不等式求出a+c的最大值,最后利用三角形两边之和大于第三边求出a+c的范围即可.
(1)∵![]() =(cos B,cos C),
=(cos B,cos C),![]() =(2a+c,b),且
=(2a+c,b),且![]() ⊥
⊥![]() .
.
∴(2a+c)cos B+bcos C=0,∴cos B(2sin A+sin C)+sin Bcos C=0,
∴2cos Bsin A+cos Bsin C+sin Bcos C=0.即2cos Bsin A=-sin(B+C)=-sin A.
∵A∈(0,π),∴sin A≠0,∴cos B=-![]() .∵0<B<π,∴B=
.∵0<B<π,∴B=![]() .
.
(2)由余弦定理得
b2=a2+c2-2accos![]() π=a2+c2+ac=(a+c)2-ac≥(a+c)2-
π=a2+c2+ac=(a+c)2-ac≥(a+c)2-![]() =
=![]() (a+c)2,
(a+c)2,
当且仅当a=c时取等号.∴(a+c)2≤4,故a+c≤2.
又a+c>b=![]() ,∴a+c∈(
,∴a+c∈(![]() ,2].即a+c的取值范围是(
,2].即a+c的取值范围是(![]() ,2].
,2].


科目:高中数学 来源: 题型:
【题目】如图所示是一个正三棱台,而且下底面边长为2,上底面边长和侧棱长都为1.O与![]() 分别是下底面与上底面的中心.
分别是下底面与上底面的中心.

(1)求棱台的斜高;
(2)求棱台的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三有![]() 名学生,按性别分层抽样从高三学生中抽取
名学生,按性别分层抽样从高三学生中抽取![]() 名男生,
名男生,![]() 名女生期未某学科的考试成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图.
名女生期未某学科的考试成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图.


(1)试计算男生考试成绩的平均分![]() 与女生考试成绩的中位数(每组数据取区间的中点值);
与女生考试成绩的中位数(每组数据取区间的中点值);
(2)根据频率分布直方图可以认为,男生这次考试的成绩服从正态分布![]() ,试计算男生成绩落在区间
,试计算男生成绩落在区间![]() 内的概率及全校考试成绩在
内的概率及全校考试成绩在![]() 内的男生的人数(结果保留整数);
内的男生的人数(结果保留整数);
(3)若从抽取的![]() 名学生中考试成绩优势(
名学生中考试成绩优势(![]() 分以上包括
分以上包括![]() 分)的学生中再选取
分)的学生中再选取![]() 名学生,作学习经验交流,记抽取的男生人数为
名学生,作学习经验交流,记抽取的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
参考数据,若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 轴上的点.
轴上的点.
(1)过点![]() 作直线
作直线![]() 与
与![]() 相切,求切线
相切,求切线![]() 的方程;
的方程;
(2)如果存在过点![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,且直线
两点,且直线![]() 与
与![]() 的倾斜角互补,求实数
的倾斜角互补,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,E为PA的中点,F为BC的中点,底面ABCD是菱形,对角线AC,BD交于点O.求证:
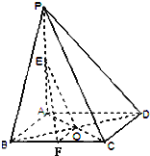
(1)平面EFO∥平面PCD;
(2)平面PAC⊥平面PBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个关于x的不等式:①![]() ;②
;②![]() ;③
;③![]()
(1)分别求出①和②的解集;
(2)若同时满足①和②的x值也满足③,求m的取值范围;
(3)若同时满足③的x至少满足①和②的一个,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com