解:(Ⅰ)S
n=
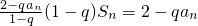
且q≠1
当n=1时,(1-q)S
1=2-qa
1?a
1=2
当n≥2时,(1-q)S
n-(1-q)S
n-1=qa
n-1-qa
n?a
n=qa
n-1∴{a
n}是以2为首项,公比为q的等比数列.
(Ⅱ) 当q=

时,由(1)得 a
n=2

又 f(x)=
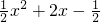
,∴f′(x)=x+2
由b
n+1=f′(b
n)得b
n+1=f′(b
n)=b
n+2
∴{b
n}是以2为首项,公差为2的等差数列,
故b
n=2n
∴c
n=
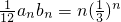
T
n=
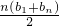
=n(n+1),
B
n=
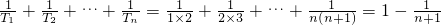
A
n=c
1+c
2+…+c
n=1•

+
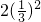
+…+
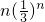
…①
∴
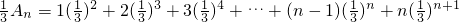
…②
①-②得∴
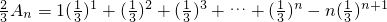
=
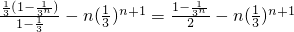
∴

∴
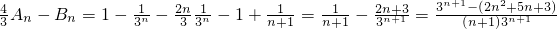
当n=1时,
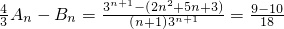
<0
∴
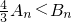
当n≥2时,
令g(x)=3
x+1-(2x
2+5x+3)
则g′(x)=3
x+1ln3-(4x+5),g
∥(x)=3
x+1(ln3)
2-4在[2,+∞)上为单调增函数,
∴g
∥(x)=3
x+1(ln3)
2-4≥3
3(ln3)
2-4>0
∴g′(x)=3
x+1ln3-(4x+5)在[2,+∞)上为单调增函数,
g′(x)=3
x+1ln3-(4x+5)≥3
3ln3-9>27-9>0
g(x)=3
x+1-(2x
2+5x+3)在[2,+∞)上为单调增函数,
∴当n≥2时,g(n)=3
n+1-(2n
2+5n+3)≥3
3-(2×4+10+3)>0
即当n≥2时,
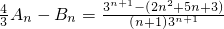
>0
∴当n≥2时,
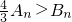
又f′(x)=x+2>0对x≥0恒成立,
∴f(x)在[0,+∞)上单调递增,
∴当n=1时f(
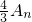
)<f(B
n)
当n≥2时f(
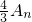
)>f(B
n).
分析:(I)利用n≥2时,数列的通项a
n与前n项和S
n的关系可得a
n=qa
n-1,再根据等差,等比数列的定义判断即可.
(II)先求出{a
n}与{b
n}的通项公式,从而得到{c
n}的通项以及Tn,然后利用裂项求和法求出B
n,利用错位相消法求出A
n,再将
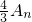
与B
n作差比较即可.
点评:本题主要考查了数列与不等式的综合,同时考查了裂项求和法和错位相消法的运用,属于难题.

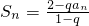 (n∈N*)其中q为非零常数,函数
(n∈N*)其中q为非零常数,函数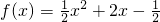 ,数列{bn}满足bn+1=f′(bn),(n∈N*),b1=f(1),设
,数列{bn}满足bn+1=f′(bn),(n∈N*),b1=f(1),设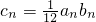 ,{bn}的前n项和为Tn,
,{bn}的前n项和为Tn,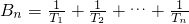 ,求An=c1+c2+…+cn.
,求An=c1+c2+…+cn. 时,试比较
时,试比较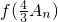 与f(Bn)的大小,并说明理由.
与f(Bn)的大小,并说明理由.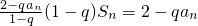 且q≠1
且q≠1 时,由(1)得 an=2
时,由(1)得 an=2
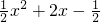 ,∴f′(x)=x+2
,∴f′(x)=x+2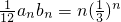 Tn=
Tn=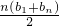 =n(n+1),
=n(n+1),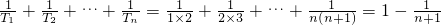
 +
+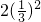 +…+
+…+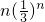 …①
…①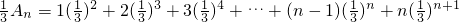 …②
…②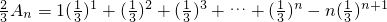
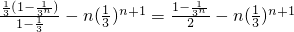

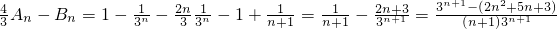
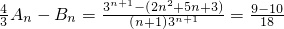 <0
<0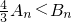
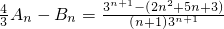 >0
>0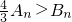
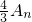 )<f(Bn)
)<f(Bn)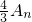 )>f(Bn).
)>f(Bn).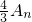 与Bn作差比较即可.
与Bn作差比较即可.
