练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若随机向一个边长为1的正三角形内丢一粒豆子（假设该豆子一定落在三角形内），则豆子落在此三角形内切圆内的概率是
    		3
    π
    9
    		3
    π
    9
    ．
    分析：由于三角形的边长为1，则内切圆半径为
    		3
    6
    ，然后求出三角形面积及其内切圆的面积，代入几何概型公式，即可得到答案．
    解答：解：∵正三角形的边长为1，
    ∵正三角形的面积S三角形=
    		3
    4
    ×12=
    		3
    4

    其内切圆半径为
    		3
    6
    ，内切圆面积S圆=πr2=
    1
    12
    π
    故向正三角形内撒一粒豆子，则豆子落在圆内的概率P=
    S圆
    S正三角形
    =
    		3
    π
    9
    ．
    故答案为：
    		3
    π
    9
    ．
    点评：本题主要考查了几何概型，以及圆与正三角形的面积的计算，解题的关键是弄清几何测度，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

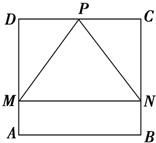
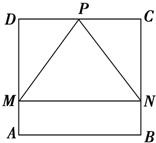    精英家教网如图，四边形ABCD是一个边长为1的正方形，△MPN是正方形的一个内接正三角形，且MN∥AB，若向正方形内部随机投入一个质点，则质点恰好落在△MPN的概率为（　　）
    A、
    1
    2
    B、
    		3
    2
    C、
    		3
    3
    D、
    		3
    4

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图，四边形ABCD是一个边长为1的正方形，△MPN是正方形的一个内接正三角形，且MN∥AB，若向正方形内部随机投入一个质点，则质点恰好落在△MPN的概率为（　　）
    A．
    1
    2
    		B．
    		3
    2
    		C．
    		3
    3
    		D．
    		3
    4
    精英家教网

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分14分）

    Monte-Carlo方法在解决数学问题中有广泛的应用。下面是利用Monte-Carlo方法来计算定积分。考虑定积分，这时等于由曲线，轴，所围成的区域M的面积，为求它的值，我们在M外作一个边长为1正方形OABC。设想在正方形OABC内随机投掷个点，若个点中有个点落入中，则的面积的估计值为，此即为定积分的估计值I。向正方形中随机投掷10000个点，有个点落入区域M

    (1)若=2099，计算I的值，并以实际值比较误差是否在5%以内

    (2)求的数学期望

    (3)用以上方法求定积分，求I与实际值之差在区间（—0.01,0.01）的概率

    附表：

    n

    1899

    1900

    1901

    2099

    2100

    2101

    P(n)

    0.0058

    0.0062

    0.0067

    0.9933

    0.9938

    0.9942

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若随机向一个边长为1的正三角形内丢一粒豆子(假设该豆子一定落在三角形内), 则豆子落在此三角形内切圆内的概率是_______.

    查看答案和解析>>

    同步练习册答案