练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．现有10张奖券，其中4张有奖，若有4人购买，每人一张，至少有一人中奖的概率是$\frac{13}{14}$．

    分析 由题意知本题是一个古典概型，试验包含的所有事件是从10张奖券中抽4张，满足条件的事件的对立事件是没有人中奖，根据古典概型公式和对立事件的公式得到概率．

    解答 解：由题意知本题是一个古典概型，
    试验包含的所有事件是从10张奖券中抽4张共有C104=210，
    满足条件的事件的对立事件是没有人中奖，
    没有人中奖共有C64=15种结果，
    根据古典概型公式和对立事件的公式得到概率1-$\frac{15}{210}$=$\frac{13}{14}$，
    给答案为：$\frac{13}{14}$

    点评 考查运用概率知识解决实际问题的能力，对立事件是指同一次试验中，不会同时发生的事件，遇到求用至少来表述的事件的概率时，往往先求它的对立事件的概率

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．设a∈R，则1+a+a2+…+an的值为（　　）
    A．$\frac{1-{a}^{n}}{1-a}$B．$\frac{1-{a}^{n+1}}{1-a}$C．$\frac{1-{a}^{n+1}}{1-a}$或n+1D．以上都不是

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

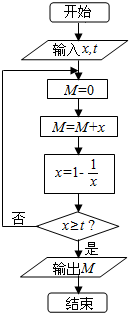
    11．执行如图所示的程序框图，如果输入的x，t均为2，则输出的M等于（　　）
    A．$\frac{1}{2}$B．$\frac{3}{2}$C．$\frac{5}{2}$D．$\frac{7}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设函数f（x）=lnx+x2-2ax+a2，a属于R．
    （1）讨论函数f（x）极值点的情况；
    （2）若函数f（x）在[$\frac{1}{2}$，2]上不是单调函数．试求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知椭圆$\frac{x^2}{2}$+y2=1与直线y=x+m交于A、B两点，且|AB|=$\frac{4\sqrt{2}}{3}$，则实数m的值为（　　）
    A．±1B．±$\frac{1}{2}$C．$\sqrt{2}$D．±$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．函数f（x）=$\sqrt{3x-{x}^{2}}$的定义域为（　　）
    A．[0，$\frac{3}{2}$]B．[0，3]C．[-3，0]D．（0，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．化简：（-3a${\;}^{\frac{1}{3}}$•b${\;}^{\frac{2}{3}}$）（a${\;}^{\frac{1}{2}}$•b${\;}^{\frac{1}{2}}$）÷（-2a${\;}^{\frac{5}{6}}$•b${\;}^{\frac{1}{6}}$）=$\frac{3}{2}b$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若y=log2x＞1，则x的取值范围是（2，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．运行如图所示的伪代码，则输出的结果S为9．

    查看答案和解析>>

    同步练习册答案