④
分析:对于①,利用向量加法的平行四边形法则得出

的坐标,从而求出
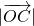 2
2=16+(k+1)
2,当且仅当k=-1时,
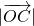
取得最小值;故①错;对于②,当k=2时,到A和点B等距离的动点P(x,y,z)的轨迹方程为线段AB的中垂面,其轨迹是一个平面;故②错;③若
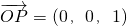
,要使得三棱锥O-ABP体积的最大,只须S
△OAB最大即可,下面求出其最大值即可.④若

=(0,0,1),则三棱锥O-ABP各个面都为直角三角形,只须在三角形OAB中,∠OAB为直角即可,再探讨在什么情况下其是直角结合概率公式计算即得.
解答:

=

+

=(1,k,0)+(3,1,0)=(4,k+1,0),
∴
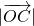 2
2=16+(k+1)
2,当且仅当k=-1时,
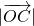
取得最小值;故①错;
对于②,当k=2时,到A和点B等距离的动点P(x,y,z)的轨迹方程为线段AB的中垂面,其轨迹是一个平面;故②错;
③若
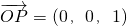
,要使得三棱锥O-ABP体积的最大,
由于三棱锥O-ABP体积=

×|

|×S
△OAB=

S
△OAB,
故只须S
△OAB最大即可,
在xOy平面内考虑,
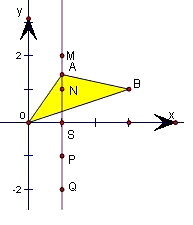
此时A(1,2),cos∠AOB=
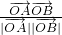
=
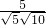
=

,∴∠AOB=45°.
S
△OAB最大=

×|

|×|

|sin∠AOB=

×

×

sin45°=

.故错;
④若

=(0,0,1),则要使得三棱锥O-ABP各个面都为直角三角形,
只须在三角形OAB中,∠OAB为直角即可,
如图,由于点A只能在M,N,S,P,Q五点取得,有5种取法,
而使得∠OAB为直角的点是M,Q,有2种取法,
则三棱锥O-ABP各个面都为直角三角形的概为

.正确.
其中,所有正确结论的应是④.
故答案为:④.
点评:本小题主要考查命题的真假判断与应用、三棱锥的几何特征、向量的数量积等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

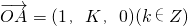 ,
,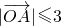 ,
,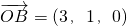 ,O为坐标原点,给出以下结论:①以OA、OB为邻边的平行四边形OACB中,当且仅当k=2时,
,O为坐标原点,给出以下结论:①以OA、OB为邻边的平行四边形OACB中,当且仅当k=2时,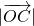 取得最小值;②当k=2时,到A和点B等距离的动点P(x,y,z)的轨迹方程为4x-2y-5=0,其轨迹是一条直线;③若
取得最小值;②当k=2时,到A和点B等距离的动点P(x,y,z)的轨迹方程为4x-2y-5=0,其轨迹是一条直线;③若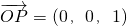 ,则三棱锥O-ABP体积的最大值为
,则三棱锥O-ABP体积的最大值为 ;④若
;④若 =(0,0,1),则三棱锥O-ABP各个面都为直角三角形的概率为
=(0,0,1),则三棱锥O-ABP各个面都为直角三角形的概率为 .其中,所有正确结论的应是________.
.其中,所有正确结论的应是________. 的坐标,从而求出
的坐标,从而求出 2=16+(k+1)2,当且仅当k=-1时,
2=16+(k+1)2,当且仅当k=-1时,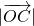 取得最小值;故①错;对于②,当k=2时,到A和点B等距离的动点P(x,y,z)的轨迹方程为线段AB的中垂面,其轨迹是一个平面;故②错;③若
取得最小值;故①错;对于②,当k=2时,到A和点B等距离的动点P(x,y,z)的轨迹方程为线段AB的中垂面,其轨迹是一个平面;故②错;③若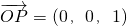 ,要使得三棱锥O-ABP体积的最大,只须S△OAB最大即可,下面求出其最大值即可.④若
,要使得三棱锥O-ABP体积的最大,只须S△OAB最大即可,下面求出其最大值即可.④若 =(0,0,1),则三棱锥O-ABP各个面都为直角三角形,只须在三角形OAB中,∠OAB为直角即可,再探讨在什么情况下其是直角结合概率公式计算即得.
=(0,0,1),则三棱锥O-ABP各个面都为直角三角形,只须在三角形OAB中,∠OAB为直角即可,再探讨在什么情况下其是直角结合概率公式计算即得. =
= +
+ =(1,k,0)+(3,1,0)=(4,k+1,0),
=(1,k,0)+(3,1,0)=(4,k+1,0),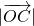 2=16+(k+1)2,当且仅当k=-1时,
2=16+(k+1)2,当且仅当k=-1时,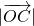 取得最小值;故①错;
取得最小值;故①错;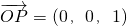 ,要使得三棱锥O-ABP体积的最大,
,要使得三棱锥O-ABP体积的最大, ×|
×| |×S△OAB=
|×S△OAB= S△OAB,
S△OAB, 此时A(1,2),cos∠AOB=
此时A(1,2),cos∠AOB=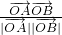 =
=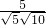 =
= ,∴∠AOB=45°.
,∴∠AOB=45°. ×|
×| |×|
|×| |sin∠AOB=
|sin∠AOB= ×
× ×
× sin45°=
sin45°= .故错;
.故错; =(0,0,1),则要使得三棱锥O-ABP各个面都为直角三角形,
=(0,0,1),则要使得三棱锥O-ABP各个面都为直角三角形, .正确.
.正确.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 满足
满足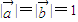 ,且
,且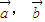 的夹角为
的夹角为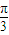 ,O为空间直角坐标系的原点,点A、B满足
,O为空间直角坐标系的原点,点A、B满足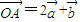 ,
,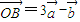 ,则△OAB的面积为( )
,则△OAB的面积为( )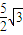
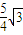
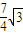
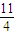
 ,
, ,
, ,O为坐标原点,给出以下结论:①以OA、OB为邻边的平行四边形OACB中,当且仅当k=2时,
,O为坐标原点,给出以下结论:①以OA、OB为邻边的平行四边形OACB中,当且仅当k=2时, 取得最小值;②当k=2时,到A和点B等距离的动点P(x,y,z)的轨迹方程为4x-2y-5=0,其轨迹是一条直线;③若
取得最小值;②当k=2时,到A和点B等距离的动点P(x,y,z)的轨迹方程为4x-2y-5=0,其轨迹是一条直线;③若 ,则三棱锥O-ABP体积的最大值为
,则三棱锥O-ABP体积的最大值为 ;④若
;④若 =(0,0,1),则三棱锥O-ABP各个面都为直角三角形的概率为
=(0,0,1),则三棱锥O-ABP各个面都为直角三角形的概率为 .其中,所有正确结论的应是 .
.其中,所有正确结论的应是 .