Question

【题目】已知函数f（x）．

（1）画出函数f（x）的图象，根据图象直接写出f（x）的值域；

（2）根据图象直接写出满足f（x）≥2的所有x的集合；

（3）若f（x）的递减区间为（﹣∞，a），递增区间为（b，+∞），直接写出a的最大值，b的最小值．

Answer 1

【答案】（1）图见解析，值域为：[0，+∞）；（2）（﹣∞，﹣1]∪[1，+∞）；（3）a的最大值为0，b的最小值为0．

【解析】

（1）根据分段函数解析式，画出函数图象，并根据图象求得函数的值域.

（2）根据图象，求得不等式的解集.

（3）根据图象，由图求得函数的单调区间，进而求得的最大值和的最小值.

（1）因为函数f（x）．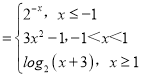

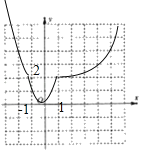
所以：函数f（x）的图象如图：；由图可知其值域为：[0，+∞）；

（2）满足f（x）≥2的所有x的集合是：（﹣∞，﹣1]∪[1，+∞）；

（3）因为函数的递减区间为：（﹣∞，0]；递增区间为：[0，+∞）；

f（x）的递减区间为（﹣∞，a），递增区间为（b，+∞）

∴a的最大值为0，b的最小值为0．