
【题目】(1)选修4-2:矩阵与变换
求矩阵![]() 的特征值和特征向量.
的特征值和特征向量.
(2)选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的方程为
的方程为![]() ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,圆
轴的正半轴建立平面直角坐标系,圆![]() 的参数方程
的参数方程![]() (
(![]() 是参数),若圆
是参数),若圆![]() 与圆
与圆![]() 相切,求实数
相切,求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)若a=1,求曲线f(x)在点(e,f(e))处的切线方程;
(Ⅱ)求f(x)的极值;
(Ⅲ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
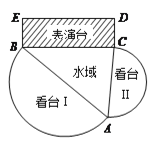
【题目】在一水域上建一个演艺广场.演艺广场由看台Ⅰ,看台Ⅱ,三角形水域![]() ,及矩形表演台
,及矩形表演台![]() 四个部分构成(如图).看台Ⅰ,看台Ⅱ是分别以
四个部分构成(如图).看台Ⅰ,看台Ⅱ是分别以![]() ,
, ![]() 为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍;矩形表演台
为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍;矩形表演台![]() 中,
中, ![]() 米;三角形水域
米;三角形水域![]() 的面积为
的面积为![]() 平方米.设
平方米.设![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的长;
的长;
(Ⅱ)若表演台每平方米的造价为![]() 万元,求表演台的最低造价.
万元,求表演台的最低造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856308)(12分)
如图,∠ABC=![]() ,O为AB上一点,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.
,O为AB上一点,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.
(Ⅰ)求证:平面PBD⊥平面COD;
(Ⅱ)求点O到平面BDC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856336)[选修4-5:不等式选讲]
已知函数f(x)=![]() -
-![]() .
.
(Ⅰ)解不等式:f(x)<2;
(Ⅱ)若x∈R,f(x)≥t2-![]() t恒成立,求实数t的取值范围.
t恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:关于x的二次方程x2+(a+1)x+a-2=0的一个根大于零,另一根小于零;命题q:不等式2x2+x>2+ax对x∈(-∞,-1)恒成立.如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com