
【题目】已知命题![]() :函数
:函数![]() 在
在![]() 上单调递增;命题
上单调递增;命题![]() :函数
:函数![]() 在
在![]() 上单调递减.
上单调递减.
(Ⅰ)若![]() 是真命题,求实数
是真命题,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() 或
或![]() 为真命题,
为真命题,![]() 且
且![]() 为假命题,求实数
为假命题,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】罗马数字是欧洲在阿拉伯数字传入之前使用的一种数码,它的产生标志着一种古代文明的进步.罗马数字的表示法如下:
数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
形式 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Ⅷ | Ⅸ |
其中“Ⅰ”需要1根火柴,“Ⅴ”与“X”需要2根火柴,若为0,则用空位表示. (如123表示为![]() ,405表示为
,405表示为![]() )如果把6根火柴以适当的方式全部放入下面的表格中,那么可以表示的不同的三位数的个数为( )
)如果把6根火柴以适当的方式全部放入下面的表格中,那么可以表示的不同的三位数的个数为( )
![]()
A.87B.95C.100D.103
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的焦点,若点
的焦点,若点![]() 在抛物线
在抛物线![]() 上,且
上,且![]()
![]() 求抛物线
求抛物线![]() 的方程;
的方程;
![]() 动直线
动直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() 其中
其中![]() ,使得向量
,使得向量![]() 与向量
与向量![]() 共线
共线![]() 其中
其中![]() 为坐标原点
为坐标原点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .现以极点
.现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为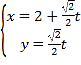 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标系方程和直线
的直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)点![]() 在曲线
在曲线![]() 上,且到直线
上,且到直线![]() 的距离为
的距离为![]() ,求符合条件的
,求符合条件的![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知等腰直角三角形![]() 的斜边
的斜边![]() 所在直线方程为
所在直线方程为![]() ,其中
,其中![]() 点在
点在![]() 点上方,直角顶点
点上方,直角顶点![]() 的坐标为
的坐标为![]() .
.

(1)求![]() 边上的高线
边上的高线![]() 所在直线的方程;
所在直线的方程;
(2)求等腰直角三角形![]() 的外接圆的标准方程;
的外接圆的标准方程;
(3)分别求两直角边![]() ,
,![]() 所在直线的方程.
所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某住宅小区为了使居民有一个优雅、舒适的生活环境,计划建一个八边形的休闲小区,其主体造型的平面图是由两个相同的矩形ABCD和矩形EFGH构成的面积是200 m2的十字形区域,现计划在正方形MNPQ上建一花坛,造价为4 200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角上铺草坪,造价为80元/m2.
(1)设总造价为S元,AD的边长为x m,试建立S关于x的函数解析式;
(2)计划至少要投多少万元才能建造这个休闲小区?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,实轴长为6,渐近线方程为
,实轴长为6,渐近线方程为![]() ,动点
,动点![]() 在双曲线左支上,点
在双曲线左支上,点![]() 为圆
为圆![]() 上一点,则
上一点,则![]() 的最小值为
的最小值为
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com