
(1)求抛物线S的方程;
(2)若O是坐标原点,P、Q是抛物线S上的两个动点,且满足OP⊥OQ.试说明动直线PQ是否过定点.
解:(1)设抛物线S的方程为y2=2px..
由 可得2y2+py-20p=0..
可得2y2+py-20p=0..
由Δ>0,有p>0,或p<-160.设B(x1,y1),C(x2,y2),则y1+y2=![]() ,
,
∴x1+x2=(5![]() )+(5
)+(5![]() )=10
)=10![]() =10+
=10+![]() ..
..
设A(x3,y3),由△ABC的重心为F(![]() ,0),则
,0),则![]() =
=![]() ,
,![]() =0,
=0,
∴x3=![]() -10,y3=
-10,y3=![]() .∵点A在抛物线S上,∴(
.∵点A在抛物线S上,∴(![]() )2=2p(
)2=2p(![]() -10).∴p=8..
-10).∴p=8..
∴抛物线S的方程为y2=16x..
(2)当动直线PQ的斜率存在时,设PQ的方程为y=kx+b,显然k≠0,b≠0,.
设P(xP,yP),Q(xQ,yQ),∵OP⊥OQ,∴kOP·kOQ=-1.∴![]() ·
·![]() =-1.
=-1.
∴xPxQ+y PyQ=0.
将y=kx+b代入抛物线方程,得ky2-16y+16b=0,
∴yPyQ=![]() .从而xPxQ=
.从而xPxQ=![]() =
=![]() ,∴
,∴![]() +
+![]() =0.
=0.
∵k≠0,b≠0,∴b=-16k.
∴动直线方程为y=kx-16k=k(x-16).此时动直线PQ过定点(16,0).
当直线PQ的斜率不存在时,显然PQ⊥x轴,又OP⊥OQ,∴△POQ为等腰直角三角形.
由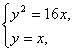
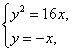 得到P(16,16),Q(16,-16).
得到P(16,16),Q(16,-16).
此时直线PQ亦过点(16,0).
综上所述,动直线PQ过定点M(16,0).


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线S的顶点在坐标原点,焦点在x轴上,![]() 的三个顶点都在抛物线上,且
的三个顶点都在抛物线上,且![]() 的重心为抛物线的焦点,若BC所在直线
的重心为抛物线的焦点,若BC所在直线![]() 的方程为
的方程为![]()
(I)求抛物线S的方程;
(II)若O是坐标原点,P,Q是抛物线S上的两动点,且满足![]() .试说明动直线PQ是否过定点.
.试说明动直线PQ是否过定点.
查看答案和解析>>
科目:高中数学 来源:2008年湖北省武汉市华中师大一附中高三五月调考数学试卷(文理合卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com