
【题目】设函数f(x)=x3﹣12x+4,x∈R.
(1)求f(x)的单调区间和极值;
(2)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围.
【答案】
(1)解:∵f(x)=x3﹣12x+4,
∴f′(x)=3x2﹣12=3(x+2)(x﹣2)
令f′(x)=0得:x1=﹣2,x2=2
当x变化时,f'(x),f(x)的变化情况如下表:
x | (﹣∞,﹣2) | ﹣2 | (﹣2,2) | 2 | (2,+∞) |
f'(x) | + | 0 | ﹣ | 0 | + |
f(x) | 增 | 极大 | 减 | 极小 | 增 |
所以f(x)的增区间是(﹣∞,﹣2)和(2,+∞),减区间是(﹣2,2);
当x=﹣2时,f(x)取得极大值,极大值f(﹣2)=20;
当x=2时,f(x)取得极小值,极小值f(2)=﹣12
(2)解:由(1)可知y=f(x)图象的大致形状及走向:
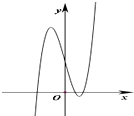
∴当﹣12<a<20时,直线y=a与y=f(x)的图象有3个不同交点,
即当﹣12<a<20时方程f(x)=a有三解
【解析】(1)求出函数的导函数,进而分析导函数在不同区间上的符号,进而根据导函数为正,对应函数的单调递增区间;导函数为负,对应函数的单调递减区间,得到f(x)的单调区间;再由左增右减对应函数的极大值,左减右增,对应函数的极小值,得到f(x)的极值;(2)由(1)作出函数f(x)的草图,进而得到方程f(x)=a有3个不同实根,可转化为a值,介于函数的两极值之间,进而得到实数a的取值范围.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的极值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=(|x﹣a2|+|x﹣2a2|﹣3a2),若对于任意x∈R,都有f(x﹣2)≤f(x),则实数a的取值范围是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子装有六张卡片,上面分别写着如下六个定义域为![]() 的函数:
的函数: ![]()
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos(θ﹣ ![]() )=1,A,B分别为C与x轴,y轴的交点.
)=1,A,B分别为C与x轴,y轴的交点.
(1)写出C的直角坐标方程,并求A,B的极坐标;
(2)设M为曲线C上的一个动点, ![]() =λ
=λ ![]() (λ>0),|
(λ>0),| ![]() ||
|| ![]() |=2,求动点Q的极坐标方程.
|=2,求动点Q的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市出租车收费标准如下:①起步价3km(含3km)为10元;②超过3km以外的路程按2元/km收费;③不足1km按1km计费.
(1)试写出收费y元与x(km)(0<x≤5)之间的函数关系式;
(2)若某人乘出租车花了24元钱,求此人乘车里程xkm的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() ,焦点
,焦点![]() ,
, ![]() 为坐标原点,直线
为坐标原点,直线![]() (不垂直
(不垂直![]() 轴)过点
轴)过点![]() 且与抛物线
且与抛物线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若![]() 为线段
为线段![]() 的中点,射线
的中点,射线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com