
【题目】设![]() ,(
,(![]() )是任意的和为正数的
)是任意的和为正数的![]() 个不同的实数,(
个不同的实数,(![]() .)是这
.)是这![]() 个数的一个排列.若对任意的
个数的一个排列.若对任意的![]() ,有
,有![]() ,则称(
,则称(![]() )是一个“好排列”.求好排列个数的最小值.
)是一个“好排列”.求好排列个数的最小值.
【答案】![]()
【解析】
一方面,当![]() ,吨,
,吨,![]() 均小于0时,易知好排列个数为
均小于0时,易知好排列个数为![]() .
.
先证明:好排列个数的最小值就是![]()
对任意满足条件的![]() .将
.将![]() 放在圆周上,而圆排列的个数为
放在圆周上,而圆排列的个数为![]() .
.
接下来证明:任意一个圆排列均对应于题设所求的一个好排列,且不同的圆排列对应不同的好排列.
设![]() 的一个圆排列为
的一个圆排列为![]() (约定
(约定![]() .),定义
.),定义![]() 元好排列(
元好排列(![]() )满足对任意的
)满足对任意的![]() ,
,![]() ,则(
,则(![]() )为
)为![]() 元好排列.
元好排列.
对所有的![]() ,取以
,取以![]() 为第一项的好排列
为第一项的好排列![]() ,易知这种好排列是存在的.一个正数就为1元好排列.取好排列中最长的一个,不妨设该好排列的第1项为
,易知这种好排列是存在的.一个正数就为1元好排列.取好排列中最长的一个,不妨设该好排列的第1项为![]() ,长度为
,长度为![]() ,即
,即![]() 为好排列.
为好排列.
(l)若![]() ,则结论得证.
,则结论得证.
(2)若![]() ,则由
,则由![]() 的最大性知
的最大性知![]() .
.
又![]() ,故
,故![]() .
.
设![]() 为使
为使![]() 的最小的
的最小的![]() ,
,
则![]() 且
且![]()
均为正数.故(![]() )为
)为![]() 元好排列.
元好排列.
于是,( ![]() ;
; ![]() )为长度大于l的好排列,矛盾.
)为长度大于l的好排列,矛盾.
【注】若(![]() )与(
)与(![]() )有重复项,则去掉
)有重复项,则去掉![]() 中的重复项,同样可以得到长度大于
中的重复项,同样可以得到长度大于![]() 的好排列.
的好排列.
从而,![]() .
.
因此,一个圆排列对应一个好排列.又显然不同的圆排列对应不同的好排列.
综上,好排列至少有![]() 个.
个.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点F的直线交地物线于点A.B(其中点A在第一象限),交其准线l于点C,同时点F是AC的中点
的焦点F的直线交地物线于点A.B(其中点A在第一象限),交其准线l于点C,同时点F是AC的中点
(1)求直线AB的倾斜角;
(2)求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市的教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的同学中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图(分组区间为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ),并将分数从低到高分为四个等级:
),并将分数从低到高分为四个等级:
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有340人.
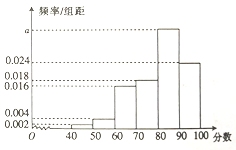
(1)求表中![]() 的值及不满意的人数;
的值及不满意的人数;
(2)在等级为不满意的师生中,老师占![]() ,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记
,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记![]() 为老师整改督导员的人数,求
为老师整改督导员的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2013支球队进行气次年度超级足球循环赛,每两支球队均恰比赛场,每场比赛胜者得3分,负者得0分,平局各得1分.比赛结束后,甲把他所在球队的总分告诉了乙,乙马上知道了甲所在球队在整个比赛中的胜负场数.试问:甲所在球队在这次比赛中所得的总分是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两地相距![]() ,汽车从甲地匀速行驶到乙地,速度不超过
,汽车从甲地匀速行驶到乙地,速度不超过![]() .已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
.已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() (单位:
(单位:![]() )的平方成正比,且比例系数为
)的平方成正比,且比例系数为![]() ,固定部分为
,固定部分为![]() 元.
元.
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() 的函数,并求出当
的函数,并求出当![]() ,
,![]() 时,汽车应以多大速度行驶,才能使得全程运输成本最小;
时,汽车应以多大速度行驶,才能使得全程运输成本最小;
(2)随着汽车的折旧,运输成本会发生一些变化,那么当![]() ,
,![]() 元,此时汽车的速度应调整为多大,才会使得运输成本最小.
元,此时汽车的速度应调整为多大,才会使得运输成本最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某歌舞团有![]() 名演员,他们编排了一些节目,每个节目都由四名演员同台表演.在一次演出中,他们发现:能适当安排若干个节目,使团中每两名演员都恰有一次在这次演出中同台表演。求
名演员,他们编排了一些节目,每个节目都由四名演员同台表演.在一次演出中,他们发现:能适当安排若干个节目,使团中每两名演员都恰有一次在这次演出中同台表演。求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上7:00至7:15之间到某公交站搭乘公交车去上学,已知在这段时间内,共有2班公交车到达该站,到站的时间分别为7:05,7:15,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com