
函数y=2|x|的值域是( )
A.(0,1] B.[1,+∞) C.(0,1) D.(0,+∞)
B
解法一:y=2|x|=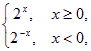 作出图象,观察得函数的值域为[1,+∞).
作出图象,观察得函数的值域为[1,+∞).
解法二:令u=|x|≥0,则y=2u≥20=1.
绿色通道 本题是一道函数综合题,需利用函数的有关性质,如求函数的定义域、值域,判断函数的奇偶性、单调性等知识.在判断函数的单调性时,我们也可以采用复合函数单调性的判断方法.当x>0时,∵2x为增函数,
∴2x-1为增函数,![]() 为递减函数,-
为递减函数,-![]() 为增函数.
为增函数.
∴y=-![]() -
-![]() 在(0,+∞)上递增.一般地,函数y=f(u)和函数u=g(x),设函数y=f[g(x)]的定义域为集合A,如果在A或A的某个子区间上函数y=f(u)(称外层函数)与u=g(x)(称内层函数)单调性相同,则复合函数y=f[g(x)]在该区间上递增;如单调性相反,则复合函数y=f[g(x)]在该区间上递减(可以简记为“同增异减”).另外,记住以下结论对判断复合函数单调性很有帮助:①若函数y=f(x)递增(减),则y=-f(x)递减(增);②若函数y=f(x)在某个区间上恒为正(负)且递增(减),则y=
在(0,+∞)上递增.一般地,函数y=f(u)和函数u=g(x),设函数y=f[g(x)]的定义域为集合A,如果在A或A的某个子区间上函数y=f(u)(称外层函数)与u=g(x)(称内层函数)单调性相同,则复合函数y=f[g(x)]在该区间上递增;如单调性相反,则复合函数y=f[g(x)]在该区间上递减(可以简记为“同增异减”).另外,记住以下结论对判断复合函数单调性很有帮助:①若函数y=f(x)递增(减),则y=-f(x)递减(增);②若函数y=f(x)在某个区间上恒为正(负)且递增(减),则y=![]() 递减(增);③若函数y=f(x)递增(减),则y=f(x)+k递增(减).
递减(增);③若函数y=f(x)递增(减),则y=f(x)+k递增(减).


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 7π |
| 2 |
| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com