
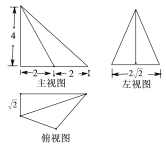
【题目】某几何体的三视图如图所示,则该几何体的外接球的表面积为_____.
【答案】![]()
【解析】
作出几何体的直观图,建立空间直角坐标系,求出外接球的球心坐标,从而可得外接球的半径,再计算出外接球的表面积.
由三视图可知几何体为四棱锥E﹣ABCD,直观图如图所示:
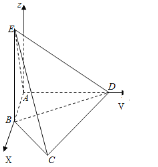
其中,BE⊥平面ABCD,BE=4,AB⊥AD,AB=![]() ,
,
C到AB的距离为2,C到AD的距离为2![]() ,
,
以A为原点,以AB,AD,及平面ABCD过A的垂线为坐标轴建立空间直角坐标系A﹣xyz,
则A(0,0,0),B(![]() ,0,0),C(2
,0,0),C(2![]() ,2,0),D(0,4,0),E(
,2,0),D(0,4,0),E(![]() ,0,4).
,0,4).
设外接球的球心为M(x,y,z),则MA=MB=MC=MD=ME,
∴x2+y2+z2=y2+(x﹣![]() )2+z2=(y﹣2)2+(x﹣2
)2+z2=(y﹣2)2+(x﹣2![]() )2+z2=(y﹣4)2+x2+z2=y2+(x﹣
)2+z2=(y﹣4)2+x2+z2=y2+(x﹣![]() )2+(z﹣4)2,
)2+(z﹣4)2,
解得y=2,x=![]() ,z=2.
,z=2.
∴外接球的半径r=MA=![]() =
=![]() ,
,
∴外接球的表面积S=4πr2=34π.
故答案为:34π


科目:高中数学 来源: 题型:
【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,说法正确的是( )
A.命题“![]() ,
,![]() ”的否定为“
”的否定为“![]() ,
,![]() ”;
”;
B.命题“在![]() 中,
中,![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
C.已知![]() 、m是两条不同的直线,
、m是两条不同的直线,![]() 是个平面,若
是个平面,若![]() ,则
,则![]() ;
;
D.已知定义在R上的函数![]() ,则“
,则“![]() 为奇函数”是“
为奇函数”是“![]() ”的充分必要条件.
”的充分必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.若
的左、右焦点.若![]() 是该椭圆上的一个动点,
是该椭圆上的一个动点,![]() 的最大值为1.
的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (
(![]() 与
与![]() 不重合),则直线
不重合),则直线![]() 与
与![]() 轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求![]() 的值;
的值;
(2)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(3)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据: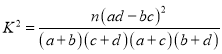 ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在极坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,弧
,弧![]() ,
,![]() 所在圆的圆心分别是
所在圆的圆心分别是![]() ,
,![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是线段
是线段![]() ,曲线
,曲线![]() 是线段
是线段![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.

(1)分别写出![]() ,
,![]() ,
,![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 由
由![]() ,
,![]() ,
,![]() ,
,![]() 构成,若点
构成,若点![]() ,(
,(![]() ),在
),在![]() 上,则当
上,则当![]() 时,求点
时,求点![]() 的极坐标.
的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中正确的命题有( )
A.设具有相关关系的两个变量x,y的相关系数为r,则![]() 越接近于0,x,y之间的线性相关程度越高
越接近于0,x,y之间的线性相关程度越高
B.随机变量![]() ,若
,若![]() ,则
,则![]()
C.公共汽车上有10位乘客,沿途5个车站,乘客下车的可能方式有![]() 种
种
D.回归方程为![]() 中,变量y与x具有正的线性相关关系,变量x增加1个单位时,y平均增加0.85个单位
中,变量y与x具有正的线性相关关系,变量x增加1个单位时,y平均增加0.85个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com